为你找到 833 个题目。
有三根铁丝,长度分别是120厘米、180厘米和300厘米。现在要把它们截成长度相等的小段,每根都不能有剩余,每小段最长为a厘米,一共可以截成b段,则a+b=( )。
A. 55
B. 65
C. 60
D. 70
E. 75
∣a-b∣=15。
(1)质数a,b满足5a+7b=99。
(2)正整数a和b的最大公约数为15,且3a+2b=180。
A. 条件(1)充分,但条件(2)不充分。
B. 条件(2)充分,但条件(1)不充分。
C. 条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分。
D. 条件(1)充分,条件(2)也充分。
E. 条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分。
某公司这周为新员工安排了 8场不同的培训课,要求每名员工从中选择4场参加.由于其中有3场安排在了同一时间,因此每名员工至多只能选择其中1场参加,那么每名员工有( )种不同的培训方案.
A. 20
B. 30
C. 35
D. 42
E. 48
二次函数y=x²+bx的图像的对称轴为x=1,则一元二次方程x²+bx-t=0在区间(-1,4)上有实数根。
(1)-1≤t≤0.
(2)7
A. 条件(1)充分,但条件(2)不充分。
B. 条件(2)充分,但条件(1)不充分。
C. 条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分。
D. 条件(1)充分,条件(2)也充分。
E. 条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分。
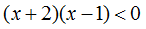 的解集为( )
的解集为( )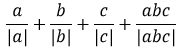 =( )。
=( )。