参考答案: D
详细解析:
本题考查黎曼可积的条件。若函数f(x)在[a,b]上(黎曼)可积,则f(x)在[a,b]上必有界(可积的必要条件),故本题选D。
下而说明其他三个选项。可积的充分条件有以下3个:①函数在闭区间上连续;②函数在闭区间上有界且只有有限个叫断点;③函数在闭区间上单调。由此可排除B项和C项。又因为在一元函数中,可微一定连续,且连续一定可积,但反之不成立,故排除A项。
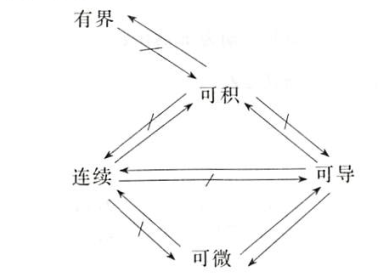
一元函数在闭区间上连续、可导、可微、可积、有界的关系图如下:
函数f(x)在[a,b]上黎曼可积的必要条件是f(x)在[a,b]上( )。
A. 可微
B. 连续
C. 不连续点个数有限
D. 有界
参考答案: D
详细解析:
本题考查黎曼可积的条件。若函数f(x)在[a,b]上(黎曼)可积,则f(x)在[a,b]上必有界(可积的必要条件),故本题选D。
下而说明其他三个选项。可积的充分条件有以下3个:①函数在闭区间上连续;②函数在闭区间上有界且只有有限个叫断点;③函数在闭区间上单调。由此可排除B项和C项。又因为在一元函数中,可微一定连续,且连续一定可积,但反之不成立,故排除A项。
一元函数在闭区间上连续、可导、可微、可积、有界的关系图如下:
