参考答案: B
详细解析:
有n个未知量的非齐次线性方程组AX=b有解的充要条件是,其系数矩阵A的秩等于其増广矩阵B的秩。而当r(A)=r(B)=n时,方程组有唯一解;当r(A)=r(B)<n时,方程组有无穷多个解;当r(A )< r(B)吋,方程组无解。
本题中,因为线性方程组 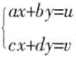 ,的系数矩阵
,的系数矩阵 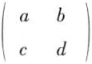 与增广矩阵
与增广矩阵 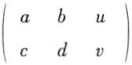 的秩均为2,且等于未知量个数,所以该方程组有唯一解。
的秩均为2,且等于未知量个数,所以该方程组有唯一解。
若矩阵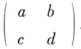 与
与 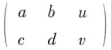 的秩均为2,则线性方程组
的秩均为2,则线性方程组 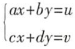 ,的解的个数是( )。
,的解的个数是( )。
A. 0
B. 1
C. 2
D. 无穷
参考答案: B
详细解析:
有n个未知量的非齐次线性方程组AX=b有解的充要条件是,其系数矩阵A的秩等于其増广矩阵B的秩。而当r(A)=r(B)=n时,方程组有唯一解;当r(A)=r(B)<n时,方程组有无穷多个解;当r(A )< r(B)吋,方程组无解。
本题中,因为线性方程组 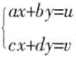 ,的系数矩阵
,的系数矩阵 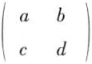 与增广矩阵
与增广矩阵 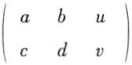 的秩均为2,且等于未知量个数,所以该方程组有唯一解。
的秩均为2,且等于未知量个数,所以该方程组有唯一解。