参考答案:
【问题1】(9分)
(1)InitQueue(&Q) (1分)注:函数名与参数必须完全正确才可得分
(2)DeQueue(&Q,&w) (2分)注:函数名与参数必须完全正确才可得分
(3)inDegree[p-> adjvex] 及其等价形式 (2分)
(4)inDegree[p->adjvex] 及其等价形式 (2分)
(5)k<G.n 或 k!=G.n (2分)
【问题2】(2分)
队列方式:v1 v2 v5 v4 v3 v7 v6(或1 2 5 4 3 7 6) (1分)
栈方式:v1 v2 v5 v4 v7 v3 v6(或1 2 5 4 7 3 6) (1分)
【问题3】(4分)
(6)O(n+e) (2分)
(7)O(n2) (2分)
详细解析:
本题考查数据结构和算法中的拓扑排序算法。
【问题1】
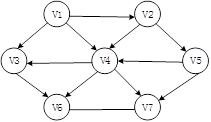
拓扑排序是将有向无环图中所有顶点排成一个线性序列的过程,并且该序列满足:若在有向图中从顶点Vi到Vj有一条路径,则在该线性序列中,顶点Vi必然在顶点Vj之前。
对AOE网进行拓扑排序的方法如下:
① 在AOE网中选择一个入度为零(没有前驱)的顶点且输出它:
② 从网中删除该顶点及其与该顶点有关的所有边;
③ 重复上述两步,直至网中不存在入度为零的顶点为止。
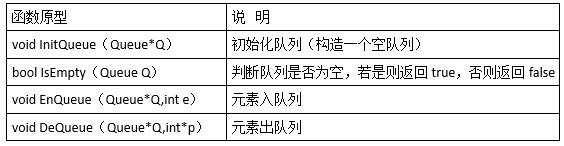
在拓扑排序过程中,需要将入度为0的顶点临时存储起来。函数中用一个队列暂存入度为0且没有进入拓扑序列的顶点。显然,空(1)处应填入InitQueue(&Q)。
进行拓扑排序之前,应先求出网中每个顶点的入度并存入数组inDegree[]中,从而将“从网中删除该顶点及其与该顶点有关的所有边”的操作转换为“相关顶点的入度减1”,一旦发现某个顶点的入度变为0,就将其编号压入堆栈。从而将选择入度为0的顶点操作转化为令队头所代表的顶点出队。
根据注释,空(2)处应填入DeQueue(&Q,&w),实现队头元素出队列的处理。
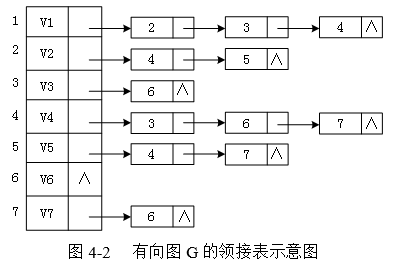
题中图采用邻接表存储结构,当指针p指向Vi邻接表中的结点时,p->adjvex表示vi的一个邻接顶点,删除vi至顶点p-> adjvex的弧的操作实现为顶点p->adjvex的入度减1,因此,空(3)处应填入inDegree[p->adjvex],当顶点p->adjvex的入度为0时,需要将其加入队列,因此空(4)处也应填入inDegree[p->adjvex]。
空(5)处判断是否所有顶点都加入了拓扑序列,算法中变量k用于对加入序列的顶点计数,因此,空(5)处应填入“k<G.n”或“k!=G.n"。
【问题2】
使用栈和队列的差别在于拓扑序列中顶点的排列次序可能不同。对于本题中的有向图,在使用队列的方式更下:
(1)开始时仅顶点V1的入度为0,因此顶点V1入队:
(2)队头顶点V1出队,并进入拓扑序列,然后删除从顶点V1出发的弧后,仅使顶点v2的入度为0,因此顶点v2入队:
(3)队头顶点v2出队,并进入拓扑序列,然后删除从顶点v2出发的弧后,仅使顶点v5的入度为0,因止顶点v5入队;
(4)队头顶点v5出队,并进入拓扑序列,然后删除从顶点v5出发的弧后,仅使顶点v4的入度为0,因此顶点v4入队;
(5)队头顶点v4出队,并进入拓扑序列,然后删除从顶点v4出发的弧后,仅使顶点v3和v7的入度为0,因此顶点v3和v7依次入队;
(6)队头顶点v3出队,并进入拓扑序列,然后删除从顶点v3出发的弧后,没有产生新的入度为0的顶点;
(7)队头顶点v7出队,并进入拓扑序列,然后删除从顶点v7出发的弧后,使顶点v6的入度为0,因此顶点v6入队;
(8)队头顶点v6出队,并进入拓扑序列,然后删除从顶点v6出发的弧后,没有产生新的入度为0的顶点,队列已空,因此结束拓扑排序过程,得到的拓扑序列为v1 v2 v5 v4 v3 v7 v6。
使用栈保存入度为0的顶点时,前4步都是一样的,因为每次仅有一个元素进栈,因此出栈序列与入栈序列一致。到第5步时,v3和v7依次入栈后,出栈时的次序为v7和v3,因此得到的拓扑序列为v1 v2 v5 v4 v7 v3 v6。
【问题3】
以邻接表为存储结构时,计算各顶点入度的时间复杂度为O(e),建立零入度顶点队列的时间复杂度为O(n)。在拓扑排序过程中,(图中无环情况下)每个顶点进出队列各1次,入度减l的操作在while循环中共执行e次,所以总的时间复杂度为O(n+e) 。
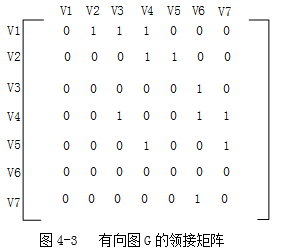
以邻接矩阵为存储结构时,计算各顶点入度时需要遍历整个矩阵,因此时间复杂度为O(n),建立零入度顶点队列的时间复杂度为O(n)。在拓扑排序过程中,(图中无环情况下)每个顶点进出队列各1次,实现入度减1操作时需遍历每个顶点的行向量1遍(时间复杂度为O(n) ),所以总的时间复杂度为O(n2)。