参考答案: C

详细解析:

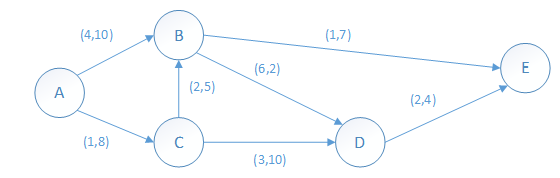
从结点A到结点E可以同时沿多条路径运输，总的最大流量应是各条路径上的最大流量之和，每条路径上的最大流量应是其各段流量的最小值。

注意本题已经给出问题的解决方案：“如果每次都选择最小费用的路径来分配最大流量，则可以用最小总费用获得最大总流量的最优运输方案。”，这里其实用到的是贪心的算法策略，最终得到的结果并不是实际最优解。

根据题干给出的策略解题时，每找出一条路径算出流量后，该路径上各段线路上的流量应扣除己经算过的流量，形成剩余流量。剩余流量为0的线段应将其删除（断开）。这种做法比较简单直观。

同时还要考虑费用问题，路径ABE每抽取1单位流量费用为5，路径ACBE每抽取1单位流量费用为4，路径ACBDE每抽取1单位流量费用为11，路径ACDE每抽取1单位流量费用为6，路径ABDE每抽取1单位流量费用为12，所以先抽取路径ACBE上的最大流量。

路径ACBE的最大流量为5万吨，计算过后，该路径上各段流量应都减少5万吨。从而BC之间将断开，AC之间的剩余流量是3万吨，BE之间的剩余流量是2万吨（如下图）。

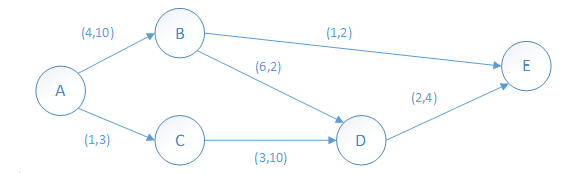
其次抽取路径ABE上的最大流量，路径ABE的最大流量为2万吨，计算过后，该路径上各段流量应都减少2万吨。从而BE之间将断开，AB之间的剩余流量是8万吨（如下图）。  

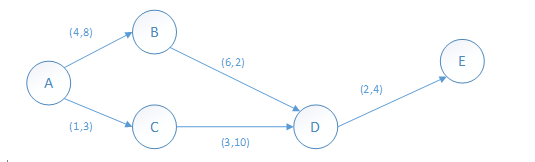
然后抽取路径ACDE上的最大流量，路径ACDE的最大流量为3万吨，计算过后，该路径上各段流量应都减少3万吨。从而AC之间将断开，CD之间的剩余流量是7万吨，DE之间的剩余流量是1万吨（如下图）。 

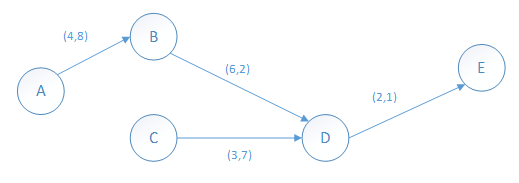
最后抽取路径ABDE上的最大流量，路径ABDE的最大流量为1万吨，计算过后，该路径上各段流量应都减少1万吨。从而DE之间将断开，AB之间的剩余流量是7万吨，BD之间的剩余流量是1万吨（如下图）。

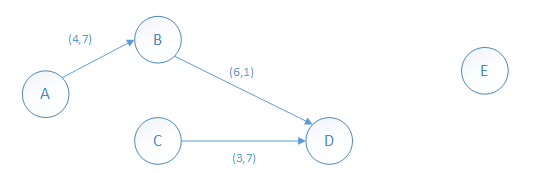
所以A到E的最大流量为5+2+3+1=11，总费用为5*4+2*5+3*6+1*12=60，答案为C选项。