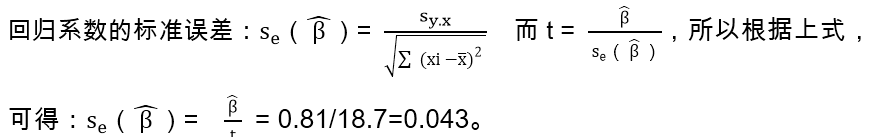参考答案: D B
详细解析:
（1）判断回归参数的显著性时应检验tα/2的计算值与临界值，当计算的tα/2大于临界值时，可拒绝原假设，得出显著性的结论。其中临界值通过查参数为（样本数-自由度）而得。
（2）
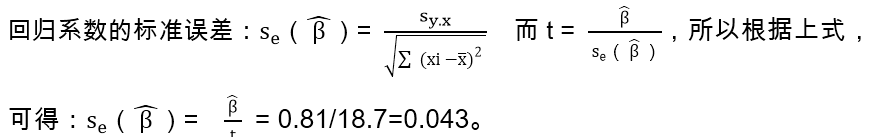
某分析师建立了一元线性回归模型为Ci=β0+β1Yi+Ui,根据已知样本，得到如下估计方程：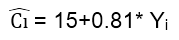
t= (13. 1) (18. 7) n=19 R2=0. 81
其中，C为消费(元)，Y为收入(元)α
已知 t0.025(19) = 2.0930，t0.05(19)=1.729 , t0.025(17) = 2.0930，t0.05(17)=1.729
（1）在显著性水平a =0.05的条件下，对于该一元回归模型的回归系数显著性分析正确的是 ( )。
（2）根据题目中提供的信息，确定参数β1的标准误差约为（ ）。
第 1 问
A. t=13.1> t0.05(17)=1.7396, β0显著不为0
B. t=13.1> t0.05(19)=1.729, β0显著不为0
C. t=18.7> t0.025(19)=2.093, β1显著不为0
D. t=18.7> t0.025(17)=2.1098, β1显著不为0
第 2 问
A. 1.145
B. 0.043
C. 0.383
D. 0.815