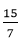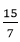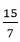方程ax2+bx+c=0有两个不同的实根。
(1)a>b>c
(2)方程ax2+bx+c=0的一个根为1
A. 条件(1)充分,但条件(2)不充分。
B. 条件(2)充分,但条件(1)不充分。
C. 条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分。
D. 条件(1)充分,条件(2)也充分。
E. 条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分。
某人参加雅思托福考试,每次考试通过的概率为P,如果他连续参加4次考试,恰好通过一次的概率为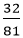 。
。
(1)他参加4次考试恰好通过2次的概率为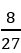 。
。
(2)他参加4次考试恰好通过3次的概率为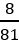 。
。
A. 条件(1)充分,但条件(2)不充分。
B. 条件(2)充分,但条件(1)不充分。
C. 条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分。
D. 条件(1)充分,条件(2)也充分。
E. 条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分。
等式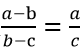 成立。
成立。
(1)a,b,c互不相等,且它们的倒数成等差数列。
(2) a,b,c互不相等,且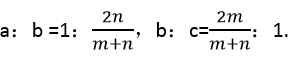
A. 条件(1)充分,但条件(2)不充分.
B. 条件(2)充分,但条件(1)不充分.
C. 条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分.
D. 条件(1)充分,条件(2)也充分.
E. 条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来也不充分.
若一元二次方程ax²+bx+c=0(a≠0)的一个根是另一个根的两倍,则a,b,c之间的关系为( )。
A. 4b²=9c
B. 4b²=9ac
C. b²=8ac
D. 4b²=7ac
E. 2b²=9ac
某批产品共有4只次品和6只正品,每只产品均不相同。现在每次取出1只产品测试,直到4只次品全部被测出为止,则最后1只次品恰好在第5次测试时被发现的不同情况有( )。
A. 576 种
B. 626 种
C. 72 种
D. 81 种
E. 124 种