参考答案: D
详细解析:
本题考查的是一元二次方程的根。求判断一元二次方程的根,利用∆=b²-4ac来判断,∆>0,有2个不同实数根;∆=0,有2个相等的实数根;∆<0,无实数根。题干中∆=4(a+b)²-4c².
条件一:a,b,c是一个三角形的三边长。构成三角形的三条边,满足任意两边之和大于第三边,任意两边之差小于第三边,则a+b>c>0,因而(a+b)²>c²,∆>0,充分。
条件二:实数a,c,b成等差数列。即2c=a+b,4c²=(a+b)²,因而∆=4(a+b)²-4c²≥0,充分。
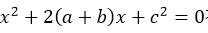 有实根。
有实根。