参考答案:
【问题1】(共8分,各2分)
(1)k ← 1 或 其等价形式
(2)cw ← cw + w[k] 或 其等价形式
(3)k ← k – 1 或 其等价形式
(4)k ← k + 1 或 其等价形式
【问题2】(共7分)
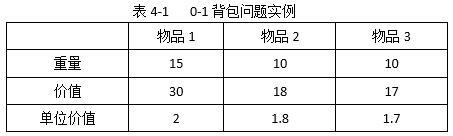
(5)物品2和物品3 (2分)
(6)35 (1分)
(7)15 (2分)
(8)8 (2分)
详细解析:
本题考查算法设计技术——回溯法。
此类题目要求考生掌握基本的算法设计技术,包括分治法、动态规划法、贪心算法、回溯法和分支限界法等,然后结合具体的问题,用对应的算法设计技术来解决问题。
【问题1】
本题考查的是用回溯法求解0-1背包问题。回溯法有两类算法框架:非递归形式和递归形式,本题采用非递归形式表示。理解回溯法的基本思想和这两类算法框架是正确解答本题的根本要求。
回溯法从第一项物品开始考虑是否应该装入背包中,因此当前考虑的物品编号k从1开始,即k←1。然后逐项往后检查,若能全部放入背包则将该项放入背包,此时背包的重量应该是当前的重量加上当前考虑物品的重量,即cw←cw+w[k],当然背包中物品的价值也为当前的价值加上当前考虑物品的价值。若己经考虑完了所有的物品,则得到一个解,判断该解是否为当前最优,若为最优,则将该解的信息放入变量fp、fw和X中。若还没有考虑完所有的物品,意味着有些物品不能放入背包,此时先判断若不将当前的物品放入背包中,则其余物品放入背包是否可能得到比当前最优解更优的解,若得不到则回溯;否则继续考虑其余的物品。
【问题2】
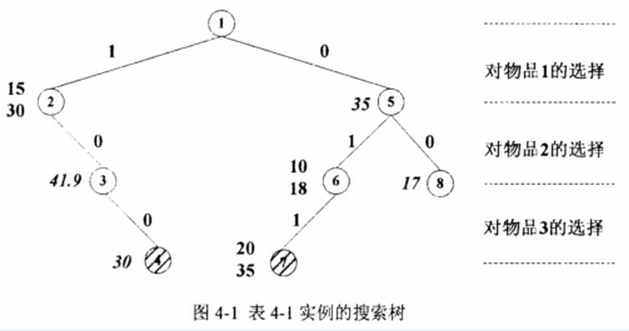
根据问题1中给出的伪代码运行该实例,可以很容易得到此0-1背包问题的最优解,应该选择物品2和物品3,此时背包的重量为10+10=20,获得的价值为17+18=35。
若采用穷举法搜索整个解空间,即要构造一颗完全二叉树,此时搜索树的结点数应为24-1=15,而采用了上述回溯法,搜索树的结点数仅为8个,如上图所示。
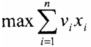 ,且总重量不超过背包容量,即
,且总重量不超过背包容量,即 ,其中,xi∈{0,1},xi=0表示第i个物品不放入背包,xi=1表示第i个物品放入背包。
,其中,xi∈{0,1},xi=0表示第i个物品不放入背包,xi=1表示第i个物品放入背包。