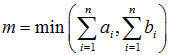参考答案:
【问题1】
(1)p[x][y][0]=1
(2)p[x][y][k]=p[x-a[k-1]][y][k-1]
(3)y- b[k -1]>=0
(4)p[x][y][n]==1或p[x][y][n]或p[x][y][n]!=0
(5)(x>=y)?x:y
【问题2】
(6) O(m2n)
【问题3】
(7)(1,1,2,2,1,1)
(8)15
详细解析:
【问题1】
下面我们来具体分析本试题。第(1)空所处的位置为schedule()函数的for循环中,从题目的描述和程序不难看出该三重循环的作用是给三维数组p赋初值,而根据题目描述可知数组k=0时,其对应的数组元素值都为1(因为这个时候没有作业,那么肯定可以在A用时不超过x且在B用时不超过y时间内处理完成),因此第1空应该填p[x][y][0]=1。
第(2)空在函数schedule()中的第二个三重for循环中,而且是在if结构下,只有if条件的结果为真时,才执行第(2)空的程序,从题目和程序也不难看出,这个三重for循环的作用就是要实现题目算法描述中的第(2)步,即求出p数组中各元素的值。那么当x - a[k-1]>=0为真时,即说明前k个作业可以在A用时不超过x内处理完成,那么根据题目意思,应该p(x,y,k)=p(x-ak,y,k-1),因此第(2)空的答案应该是p[x][y][k]=p[x-a[k-1]][y][k-1]。
第(3)空if判定的条件表达式,根据条件为真后面执行的语句可以判定出,这里的条件是要判定是否前k个作业可以在B用时不超过y内处理完成,因此第(3)空的答案是y- b[k -1]>=0,其实本题与第(2)空可以参照来完成。
第(4)空在函数write()中,是双重循环下if判定的条件,从题目注释来看,该函数是要确定最优解并输出的,那么结合该函数我们不难知识,确定最优解就是用这个双重循环来实现的,从前面的程序中,我们知道,所有的解的情况保存在数组p当中,那么现在就是要找出那个是最优解,其中max是用来存放当前最优解的,而临时变量temp要与max的值做一个比较,将较小的(当前最优)存放在max中,因此求最优解其实就是将所有解做一个比较,然后取出最优解。综上所述,再结合程序和题干描述,“用p(x,y,k)=1表示在A用时不超过x且在B用时不超过y时间内处理完成”,我们不难知道第(4)空的答案是p[x][y][n]==1或者类似的表达式,p[x][y][n]==1表示当前情况下有一个解,那么这个解是x还是y呢?这还需要接着判定x与y的值谁更小,将更小的赋值给临时变量temp,因此第5空答案为(x>=y)?x:y。
【问题2】
本题主要考查时间复杂度,相对于第一问来说,要简单很多。从给出的程序来看,最高的循环是三重循环,因此其时间复杂度为O(m2n)。
【问题3】
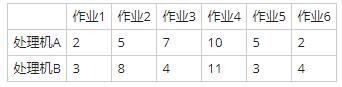
在本题给出的实例中,如果我们用题目描述的方式来求解,其过程也是相当复杂,因为在题目描述的情况下,数组p的长度为(33+1)*(33+1)*(6+1),由于我们不是计算机,要计算出该数组中各元素,肯定也不容易。在这种情况下,因为题目给出的作业只有6个,因此可以采用观察法,不难发现,本题最优解的值为15,最优解为(1,1,2,2,1,1)或者(2,1,2,1,2,2)。