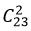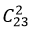参考答案: B
详细解析:
考点为相同元素的分配问题。设想24个小球排成一排,选取2块隔板任意插入其中(不能插两端),则每一种插法都对应一组解,24个球有23个空隙,任选2个空插入挡板,有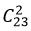
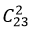
将24支相同的蜡笔分配给3个小朋友,每个小朋友至少分得1支且得到的蜡笔个数互不相同,共有( )种分配方法。
A. 200
B. 222
C. 240
D. 32
E. 36
参考答案: B
详细解析:
考点为相同元素的分配问题。设想24个小球排成一排,选取2块隔板任意插入其中(不能插两端),则每一种插法都对应一组解,24个球有23个空隙,任选2个空插入挡板,有