参考答案: B
详细解析:
本题考查的是等比数列的问题。条件(1):已知an =4n-1,则数列{an}是首项为1,公比为4的等比数列,则Sn=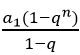 =
=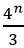 -1,不充分。
-1,不充分。
条件(2):当n=1时,T1=1;
当n≥2时,an2=Tn-Tn-1=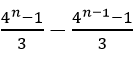 =
=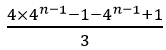 =
=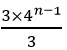 =4n-1;
=4n-1;
经检验,n=1时也满足通项公式,则an2 =
4n-1 。
又因为{an}各项均为正,则an=2n-1,数列{an}是首项为1,公比为2的等比数列,所以Sn=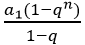 =
=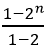 =2n-1,充分。
=2n-1,充分。
已知数列{an}的前n项和为Sn,则Sn=2n-1。
(1)数列{an}的通项公式为an =4n-1。
(2)数列{an}各项均为正,且数列{an2}的前n项和为Tn=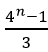 。
。
A. 条件(1)充分,但条件(2)不充分。
B. 条件(2)充分,但条件(1)不充分。
C. 条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分。
D. 条件(1)充分,条件(2)也充分。
E. 条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分。
参考答案: B
详细解析:
本题考查的是等比数列的问题。条件(1):已知an =4n-1,则数列{an}是首项为1,公比为4的等比数列,则Sn=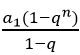 =
=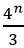 -1,不充分。
-1,不充分。
条件(2):当n=1时,T1=1;
当n≥2时,an2=Tn-Tn-1=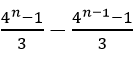 =
=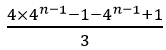 =
=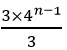 =4n-1;
=4n-1;
经检验,n=1时也满足通项公式,则an2 =
4n-1 。
又因为{an}各项均为正,则an=2n-1,数列{an}是首项为1,公比为2的等比数列,所以Sn=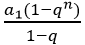 =
=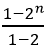 =2n-1,充分。
=2n-1,充分。