参考答案: C

详细解析:

该企业厂区、生活区以及河道的位置可以图示如下。

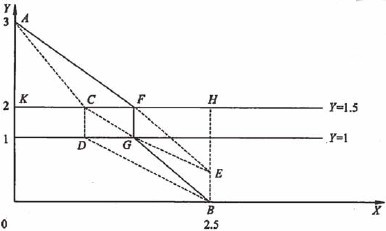
上图中，A点表示厂区，B点表示生活区，垂直于河岸的CD表示建桥的某种方案。本题希望调整CD点的位置使总距离AC+CD+DB最小。由于CD恒为0.5 km，所以关键是要使AC+DB最短。将DB平移到CE，则E点是确定的，坐标为（2.5，0.5）。问题变成在直线Y=1.5上取点C，使它到定点A与E的距离之和最小。显然，直线AE与Y=1.5的交点F，到达A点与E点的距离之和最小（因为AC+CE≥AE）。在F处建桥FG。则AF+FG+GB=AF+0.5+FE=AE+0.5将使距离最短。
为计算F点的坐标，延长BE到H（与直线Y=1.5的交点）。由于AK =1.5，EH=1，KH=2.5，所以KF=1.5，FH=1。这样，桥应建在坐标X=1.5 km处。
本题如用代数方法计算则比较麻烦。
本题也可以根据4种选择答案算出4种距离，选择最小的一种为正确答案，但这种方法只是应试技巧，实际应用中并没有提供选择答案。