参考答案: A

详细解析:

三次多项式Y=f(x)的曲线有以下几个特征：
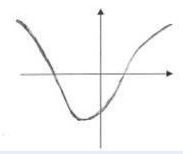
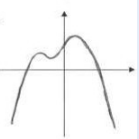
（1）三次多项式的定义域与值域均为（-∞，+∞），所以，值域不能覆盖整个数轴的选择答案C与D应排除。
（2）三次多项式力f(x)曲线与水平线Y=a（ a为任意常数）的交点数，应等于三次方程f(x)-a=0的实根数，所以，一定为l， 2或3，不可能是0，也不可能超过3。根据该特征，也可以排除选择答案C，D。
（3）x→-∞或x→-+∞时，三次多项f(x)的值也会趋于无穷，而且会在一端趋于-∞，另一端趋于+∞。根据该特征，同样可以排除选择答案C、D。
（4）三次多项式的导函数f’(x)为二次多项式，其二阶导函数f’’(x)为一次多项式。f’(x)的正负性描述了f(x)曲线的递增递减性，f’’(x)的正负性体现了f(x)曲线的凹凸性。
由于f’(x)为二次函数，其正负性的变化至多改变2次，因此三次多项式的递增、递减情况也最多改变2次（从直观看，升降性最多分三段）。
由于f’’(x)为一次函数（线性），其正负性至多改变一次，因此三次多项式的凹凸性也至多改变一次。
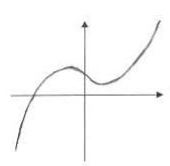
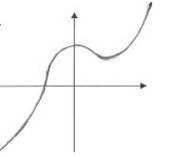
选择答案A与B中，f(x)曲线从左到右都是先递增，再递减，又递增，改变了2次。
选择答案A中，f(x)曲线的凹凸性变化从左到右为先凸，再凹，改变了1次。
选择答案B中，f(x)曲线的凹凸性变化从左到右为先凹，再凸，又凹，改变了2次，因此，不符合三次多项式的特征。
从而，选择答案B，C，D都不可能是三次多项式曲线。