参考答案: B

详细解析:

答案：B
【考点判断】绝对值不等式
【解题必知】
①绝对值不等式性质：若|x|≤a，则：-a≤x≤a
②ax²+bx+c≤0的解集为空集，只需满足

【解题思路】利用绝对值不等式的性质将不等式转化为两个一元二次不等式，再用不等式恒成立解决。
【解题步骤】
|x²+2x+a|≤1，即-1≤x²+2x+a≤1，

即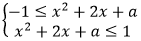要同时成立，下面可以借用二次函数来理解，

对于二次函数y=x²+2x+a，开口向上函数图像可以无限往上延伸，故无论a为何值，y=x²+2x+a≥-1一定有解；

所以只能是x²+2x+a≤1无解，

即x²+2x+a>1恒成立，进一步得x²+2x+a-1>0恒成立。

所以只要∆=2²-4×1×(a-1)<0(用函数观点解释为：二次函数开口向上，且<>0，即函数与x轴无交点，则函数图像全部在x轴上方，即y>0恒成立)

解得：a>2，
条件(1)： a<0不在a>2范围内，条件不充分，
条件(2)：a>2满足条件，条件充分。选B。