参考答案: D

详细解析:

答案：D
【考点判断】根的判别式应用
【解题必知】求函数的交点，即要联立函数的解析式解方程。二次函数与一次函数相切，即两个函数只有一个交点，即联立得到的一元二次方程有两个相同的解解，即∆=0。
【解题思路】联立函数解析式，利用∆=0求解。
【解题步骤】
一、判断条件(1)，代入题干，即判断“已知二次函数f(x)=x²+ax+b与一次函数f(x)=x+1相切，且a+b=1，则能确定a、b”是否成立。

联立函数解析式：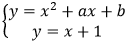
消去y得：x²+ax+b=x+1，整理得：x²+(a-1)x+b-1=0

由两个函数相切得，该方程∆=(a-1)²-4(b-1)=0，整理得：a²-2a-4b+5=0

因a+b=1，则b=1-a，将其带入a²-2a-4b+5=0中，

得a²-2a-4(1-a)+5=0，即(a+1)²=0，解得：a=-1，b=2，故条件充分。

二、判断条件(2)，代入题干，即判断“已知二次函数f(x)=x²+ax+b与一次函数f(x)=x+1相切，且a-b=1，则能确定a、b”是否成立。

因a-b=1，则b=a-1，将其代入a²-2a-4b+5=0中，

得a²-2a-4(a-1)+5=0，即(a-3)²=0，解得：a=3，b=2，故条件充分。选D。