参考答案: B
详细解析:
本题考查的是圆与圆的位置关系。两个圆相切可能内切也可能外切,当两个圆外切时,圆点的距离等于半径距离和,当圆内切时,圆心的距离相减的绝对值等于圆心距。已知圆C1的圆点为(1,2),半径为r,圆C2的圆点为(3,4),半径为5,分情况讨论:当圆外切时,则有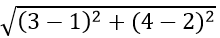 =5+r,解得r=2
=5+r,解得r=2
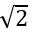 -5,因为r>0,故不存在;
-5,因为r>0,故不存在;
当圆内切时,
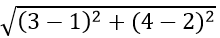 =|5-r|,|5-r|=2
=|5-r|,|5-r|=2
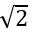 ,解得r=5±2
,解得r=5±2
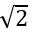 。因此条件(1)不充分,条件(2)充分。
。因此条件(1)不充分,条件(2)充分。
圆C1:(x-1)2+(y-2)2=r2 (r>0)与圆C2:(x-3)2+(y-4)2=25相切。
(1) r=5±2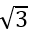
(2) r=5±2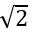
A. 条件(1)充分,但条件(2)不充分。
B. 条件(2)充分,但条件(1)不充分。
C. 条件(1)和条件(2)单独都不充分,但条件(1)和条件(2)联合起来充分。
D. 条件(1)充分,条件(2)也充分。
E. 条件(1)和条件(2)单独都不充分,条件(1)和条件(2)联合起来也不充分。
参考答案: B
详细解析:
本题考查的是圆与圆的位置关系。两个圆相切可能内切也可能外切,当两个圆外切时,圆点的距离等于半径距离和,当圆内切时,圆心的距离相减的绝对值等于圆心距。已知圆C1的圆点为(1,2),半径为r,圆C2的圆点为(3,4),半径为5,分情况讨论:当圆外切时,则有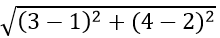 =5+r,解得r=2
=5+r,解得r=2
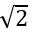 -5,因为r>0,故不存在;
-5,因为r>0,故不存在;
当圆内切时,
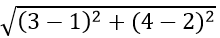 =|5-r|,|5-r|=2
=|5-r|,|5-r|=2
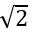 ,解得r=5±2
,解得r=5±2
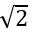 。因此条件(1)不充分,条件(2)充分。
。因此条件(1)不充分,条件(2)充分。