参考答案: C
详细解析:
本题考查的是绝对值问题。这类问题需去绝对值，常用去绝对值的方法为分类讨论和两边同时平方。
条件一：|a+b|≤1，两边同时平方得：(a+b)²≤1，若a=4，b=-3满足条件，但显然结论不成立，不充分。
条件二：|a-b|≤1，两边同时平方得：(a-b)²≤1，若a=4，b=3满足条件，但显然结论不成立，也不充分。
考虑联合，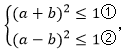
①＋②化简后得：a²+b²≤1，又因为a²≥0，b²≥0，则|a|≤1且|b|≤1，成立。
已知a,b是实数，则|a|≤1，|b|≤1
（1）|a+b|≤1. （2）|a-b|≤1.
A. 条件（1）充分，但条件（2）不充分.
B. 条件（2）充分，但条件（1）不充分.
C. 条件（1）和（2）单独都不充分，但条件（1）和条件（2）联合起来充分.
D. 条件(1)充分，条件(2)也充分.
E. 条件(1)和(2)单独都不充分，但条件(1)和条件(2)联合起来也不充分.
参考答案: C
详细解析:
本题考查的是绝对值问题。这类问题需去绝对值，常用去绝对值的方法为分类讨论和两边同时平方。
条件一：|a+b|≤1，两边同时平方得：(a+b)²≤1，若a=4，b=-3满足条件，但显然结论不成立，不充分。
条件二：|a-b|≤1，两边同时平方得：(a-b)²≤1，若a=4，b=3满足条件，但显然结论不成立，也不充分。
考虑联合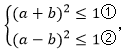，①＋②化简后得：a²+b²≤1，又因为a²≥0，b²≥0，则|a|≤1且|b|≤1，成立。