参考答案: B
详细解析:
本题考查的是线性规划问题,解题思路就是将代数问题转化成几何图象问题,主要步骤:①列出不等式组;②画出可行区域;③确定目标函数,并在可行区域内平移;④找出需要的点,代入即可。
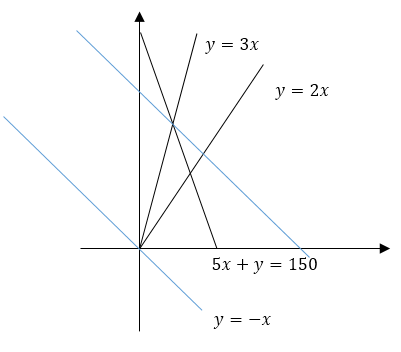
设计划投资室内车位的数量为x个,计划投资室外车位的数量为y个,根据条件列出不等式组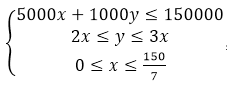 设最多可建车位的数量为z,x+y=z,即y=-x+z,因此要求z最大,即求y=-x+z的截距最大。将y=-x平移到直线5x+y=150与y=3x的交点时,此时截距最大,求出交点坐标
设最多可建车位的数量为z,x+y=z,即y=-x+z,因此要求z最大,即求y=-x+z的截距最大。将y=-x平移到直线5x+y=150与y=3x的交点时,此时截距最大,求出交点坐标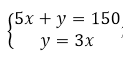 解得:?=754,因为?和?为整数,所以?取19,20,21,当?=19时,?=55时,满足条件。因此最多可建车位的数量为74个。
解得:?=754,因为?和?为整数,所以?取19,20,21,当?=19时,?=55时,满足条件。因此最多可建车位的数量为74个。