参考答案: D
详细解析:
答案:D
【考点判断】“穿线法”解高次不等式
【解题必知】分式不等式等价性: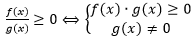
【解题思路】利用分式不等式的等价性,将不等式转化为高次不等式用“穿线法”求解,注意分母要不能为0
【解题步骤】
原不等式等价于: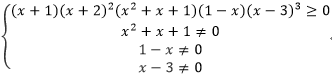
对于不等式(x+1)(x+2)2(x2+x+1)(1-x)(x-3)3≥0
系数化正,得:
(x+1)(x+2)2(x2+x+1)(x-1)(x-3)3≤0
x2+x+1对应的判别式∆=1-4<0,故x2+x+1恒为正,乘积恒为正,它对应的图像与x轴无交点,不产生根,对不等式解集无影响,可删去
原不等式等价于:(x+1)(x+2)2(x-1)(x-3)3≤0
运用“穿针引线”法解得:x∈(-∞,-1]∪[1,3]
因为1-x≠0、x-3≠0,所以x≠1、x≠3
综上,不等式得解集为:x∈(-∞,-1]∪(1,3)
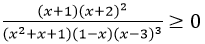 的解集为( )
的解集为( )