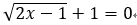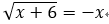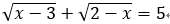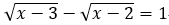参考答案: B

详细解析:

答案：B
【考点判断】根式方程
【解题必知】
根式的非负性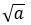： 要有意义，则a≥0

②平方去根号：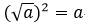
③完全平方公式：(a±b)²=a²+b²±2ab

【解题思路】多个根式的式子可移项再两边平方去根式，每次平方去掉一个根式，注意最后要验证解是否使得每个根式有意义。
【解题步骤】
A项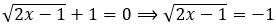：，因为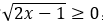，不可能等于-1，故方程无实根。

B项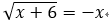：，两边平方得：x+6=x²⟹x²-x-6=0⟹(x-3)(x+2)=0

所以：x=3或x=-2，验证得：当x=3时方程不成立，故原方程有实根x=-2
C项：根据被开方数非负得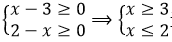：无解，故原方程无实根

D.对于任意实数x，有x-3<x-2，故在满足根式有意义的范围内√(x-3)<√(x-2)恒成立，所以√(x-3)-√(x-2)<0≠1，故方程无实根

综上所述，选B。