C++(g++ 7.5.0) 解法, 执行用时: 1181ms, 内存消耗: 884K, 提交时间: 2022-10-19 20:27:37
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
constexpr ll eps = 0;
struct point{
ll x,y;
friend bool operator !=(const point &lhs, const point &rhs){
return abs(lhs.x-rhs.x)+abs(lhs.y-rhs.y) > eps;
}
friend point operator +(const point &lhs, const point &rhs) {
return {lhs.x+rhs.x, lhs.y+rhs.y};
}
friend point operator -(const point &lhs, const point &rhs) {
return {lhs.x-rhs.x, lhs.y-rhs.y};
}
friend point operator *(const ll &k, const point &t){
return {k*t.x, k*t.y};
}
friend ll operator *(const point &lhs, const point & rhs) {
return lhs.x*rhs.y - lhs.y*rhs.x;
}
};
using ppi = pair<point, int>;
bool argcmp (const point &a, const point &b) {
const auto quad = [](const point &a) {
if(a.y < -eps) return 3;
if(a.y > eps) return 1;
if(a.x < -eps) return 2;
if(a.x > eps) return 0;
return 0;
};
const int qa = quad(a), qb = quad(b);
if(qa != qb) return qa < qb;
return a*b > eps;
};
void solve(){
int n; cin >> n;
vector<ppi>vec(n);
int n0 = 0, n1 = 0, n2 = 0;
for(int i = 0 ; i < n ; i ++){
auto &[p,c] = vec[i];
cin >> p.x >> p.y >> c;
if(c==0) n0++;
else if(c==1) n1++;
else if(c==2) n2++;
}
ll ans = 0;
auto solve = [&](const point &p, const int &c0)->void{
vector<ppi>tmp;
for(auto &[q,c]: vec){
if(q != p) tmp.push_back({q-p, c});
}
sort(tmp.begin(), tmp.end(), [](ppi &A, ppi &B){
return argcmp(A.first, B.first);
});
auto copy = tmp;
tmp.insert(tmp.end(), copy.begin(), copy.end());
int t0 = 0, t1 = 0, t2 = 0;
int m = tmp.size()/2;
for(int i = 0, j = 0; i < m && (tmp[i].first.y > eps || i==0) ; i ++){
auto &[p1,c1] = tmp[i];
if(c1==0) t0--;
else if(c1==1) t1--;
else t2--;
while(j<i+m && p1 * tmp[j].first >= 0){
if(tmp[j].second==0) t0++;
else if(tmp[j].second==1) t1++;
else t2++;
j++;
}
ll v1, v2, oc0=n0-t0, oc1=n1-t1, oc2=n2-t2;
if(c0==0) v1 = t1*t2, oc0--;
else if(c0==1) v1 = t0*t2, oc1--;
else v1 = t0*t1, oc2--;
if(c1==0) v2 = oc1 * oc2;
else if(c1==1) v2 = oc0 * oc2;
else v2 = oc0 * oc1;
ans += v1 * v2;
}
};
for(auto &[p,c]: vec){
solve(p,c);
}
cout << ans << '\n';
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
solve();
return 0;
}
C++11(clang++ 3.9) 解法, 执行用时: 1277ms, 内存消耗: 600K, 提交时间: 2020-08-03 20:51:32
#include<bits/stdc++.h>
#define ts cout<<"ok"<<endl
#define ll long long
#define hh puts("")
using namespace std;
int n,cnt[2][3],to[3005];
ll ans;
double PI=3.14159265358979323846;
struct point{
double x,y,k;
int col;
}a[3005],t[3005];
inline int read(){
int ret=0,ff=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-') ff=-1;ch=getchar();}
while(isdigit(ch)){ret=(ret<<3)+(ret<<1)+(ch^48);ch=getchar();}
return ret*ff;
}
point operator - (point A,point B){
return (point){A.x-B.x,A.y-B.y};
}
inline bool cmp(point A,point B){
return A.k<B.k;
}
inline ll calc(int x,int col){
if(col==0) return 1ll*cnt[x][1]*cnt[x][2];
else if(col==1) return 1ll*cnt[x][0]*cnt[x][2];
else if(col==2) return 1ll*cnt[x][0]*cnt[x][1];
}
signed main(){
n=read();
for(int i=1;i<=n;i++){
a[i].x=read();
a[i].y=read();
a[i].col=read();
}
for(int i=1;i<=n;i++){
int tot=0;
for(int j=1;j<=n;j++){
if(j==i) continue;
t[++tot]=a[j];
t[tot].k=atan2((a[j]-a[i]).y,(a[j]-a[i]).x);
if(t[tot].k<=0) t[tot].k+=PI;
}
memset(cnt,0,sizeof(cnt));
sort(t+1,t+tot+1,cmp);
for(int j=1;j<=tot;j++){
if(t[j].y<a[i].y||(t[j].y==a[i].y&&t[j].x>a[i].x)) to[j]=0,cnt[0][t[j].col]++;
else to[j]=1,cnt[1][t[j].col]++;
}
for(int j=1;j<=tot;j++){
cnt[to[j]][t[j].col]--;
ans+=calc(0,t[j].col)*calc(1,a[i].col)+calc(0,a[i].col)*calc(1,t[j].col);
to[j]^=1;
cnt[to[j]][t[j].col]++;
}
}
printf("%lld\n",ans>>2);
return 0;
}
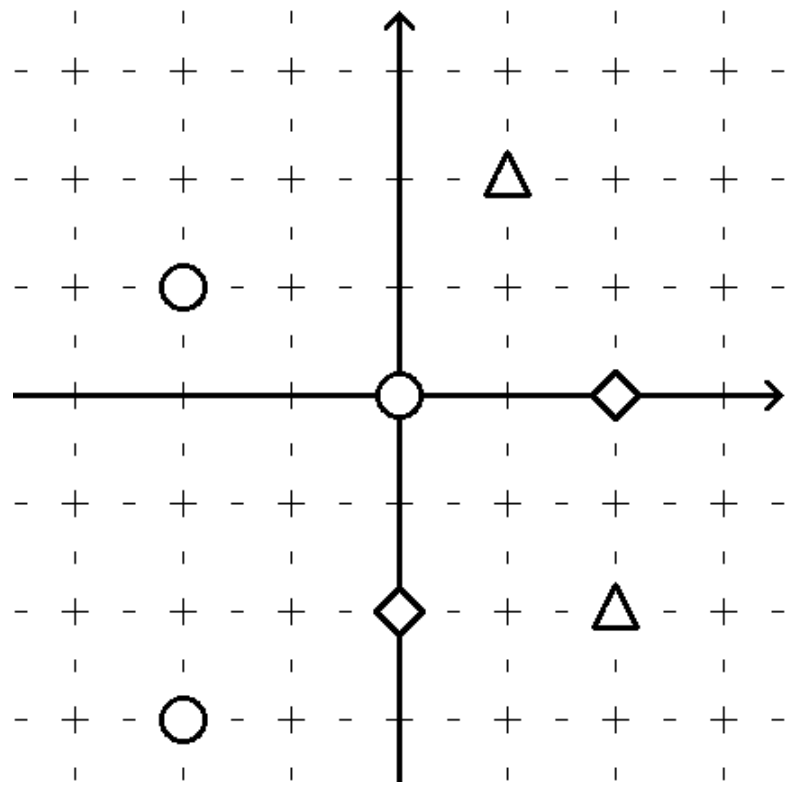
 。每颗星星的颜色为红色、蓝色、黄色中的一种。
。每颗星星的颜色为红色、蓝色、黄色中的一种。 ,位于
,位于) 。坐标系上的点两两不同,且不存在三点共线。
。坐标系上的点两两不同,且不存在三点共线。 JOI酱和IOI酱想知道构成JOIOI座的候补一共有多少种方案。
JOI酱和IOI酱想知道构成JOIOI座的候补一共有多少种方案。
,表示i号星的坐标为
,
表示i号星的颜色,其中0代表红色,1代表蓝色,2代表黄色。