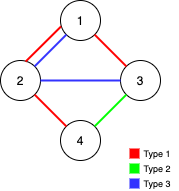
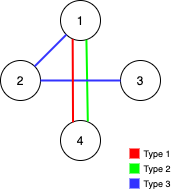
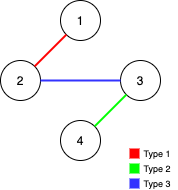
C++
Java
Python
Python3
C
C#
JavaScript
Ruby
Swift
Go
Scala
Kotlin
Rust
PHP
TypeScript
Racket
Erlang
Elixir
Dart
monokai
ambiance
chaos
chrome
cloud9_day
cloud9_night
cloud9_night_low_color
clouds
clouds_midnight
cobalt
crimson_editor
dawn
dracula
dreamweaver
eclipse
github
github_dark
gob
gruvbox
gruvbox_dark_hard
gruvbox_light_hard
idle_fingers
iplastic
katzenmilch
kr_theme
kuroir
merbivore
merbivore_soft
mono_industrial
nord_dark
one_dark
pastel_on_dark
solarized_dark
solarized_light
sqlserver
terminal
textmate
tomorrow
tomorrow_night
tomorrow_night_blue
tomorrow_night_bright
tomorrow_night_eighties
twilight
vibrant_ink
xcode
上次编辑到这里,代码来自缓存 点击恢复默认模板
class Solution {
public:
int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {
}
};
运行代码
提交
golang 解法, 执行用时: 308 ms, 内存消耗: 19.9 MB, 提交时间: 2023-09-21 10:36:05
type unionFind struct {
parent, size []int
setCount int // 当前连通分量数目
}
func newUnionFind(n int) *unionFind {
parent := make([]int, n)
size := make([]int, n)
for i := range parent {
parent[i] = i
size[i] = 1
}
return &unionFind{parent, size, n}
}
func (uf *unionFind) find(x int) int {
if uf.parent[x] != x {
uf.parent[x] = uf.find(uf.parent[x])
}
return uf.parent[x]
}
func (uf *unionFind) union(x, y int) bool {
fx, fy := uf.find(x), uf.find(y)
if fx == fy {
return false
}
if uf.size[fx] < uf.size[fy] {
fx, fy = fy, fx
}
uf.size[fx] += uf.size[fy]
uf.parent[fy] = fx
uf.setCount--
return true
}
func (uf *unionFind) inSameSet(x, y int) bool {
return uf.find(x) == uf.find(y)
}
func maxNumEdgesToRemove(n int, edges [][]int) int {
ans := len(edges)
alice, bob := newUnionFind(n), newUnionFind(n)
for _, e := range edges {
x, y := e[1]-1, e[2]-1
if e[0] == 3 && (!alice.inSameSet(x, y) || !bob.inSameSet(x, y)) {
// 保留这条公共边
alice.union(x, y)
bob.union(x, y)
ans--
}
}
uf := [2]*unionFind{alice, bob}
for _, e := range edges {
if tp := e[0]; tp < 3 && uf[tp-1].union(e[1]-1, e[2]-1) {
// 保留这条独占边
ans--
}
}
if alice.setCount > 1 || bob.setCount > 1 {
return -1
}
return ans
}
javascript 解法, 执行用时: 224 ms, 内存消耗: 72.6 MB, 提交时间: 2023-09-21 10:35:51
/**
* @param {number} n
* @param {number[][]} edges
* @return {number}
*/
// 并查集模板
class UnionFind {
constructor (n) {
this.parent = new Array(n).fill(0).map((element, index) => index);
this.size = new Array(n).fill(1);
// 当前连通分量数目
this.setCount = n;
}
findset (x) {
if (this.parent[x] === x) {
return x;
}
this.parent[x] = this.findset(this.parent[x]);
return this.parent[x];
}
unite (a, b) {
let x = this.findset(a), y = this.findset(b);
if (x === y) {
return false;
}
if (this.size[x] < this.size[y]) {
[x, y] = [y, x];
}
this.parent[y] = x;
this.size[x] += this.size[y];
this.setCount -= 1;
return true;
}
connected (a, b) {
const x = this.findset(a), y = this.findset(b);
return x === y;
}
}
var maxNumEdgesToRemove = function(n, edges) {
const ufa = new UnionFind(n), ufb = new UnionFind(n);
let ans = 0;
// 节点编号改为从 0 开始
for (const edge of edges) {
edge[1] -= 1;
edge[2] -= 1;
}
// 公共边
for (const [t, u, v] of edges) {
if (t === 3) {
if (!ufa.unite(u, v)) {
ans += 1;
} else {
ufb.unite(u, v);
}
}
}
// 独占边
for (const [t, u, v] of edges) {
if (t === 1) {
// Alice 独占边
if (!ufa.unite(u, v)) {
ans += 1;
}
} else if (t === 2) {
// Bob 独占边
if (!ufb.unite(u, v)) {
ans += 1;
}
}
}
if (ufa.setCount !== 1 || ufb.setCount !== 1) {
return -1;
}
return ans;
};
python3 解法, 执行用时: 396 ms, 内存消耗: 53.4 MB, 提交时间: 2023-09-21 10:35:36
# 并查集模板
class UnionFind:
def __init__(self, n: int):
self.parent = list(range(n))
self.size = [1] * n
self.n = n
# 当前连通分量数目
self.setCount = n
def findset(self, x: int) -> int:
if self.parent[x] == x:
return x
self.parent[x] = self.findset(self.parent[x])
return self.parent[x]
def unite(self, x: int, y: int) -> bool:
x, y = self.findset(x), self.findset(y)
if x == y:
return False
if self.size[x] < self.size[y]:
x, y = y, x
self.parent[y] = x
self.size[x] += self.size[y]
self.setCount -= 1
return True
def connected(self, x: int, y: int) -> bool:
x, y = self.findset(x), self.findset(y)
return x == y
class Solution:
def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:
ufa, ufb = UnionFind(n), UnionFind(n)
ans = 0
# 节点编号改为从 0 开始
for edge in edges:
edge[1] -= 1
edge[2] -= 1
# 公共边
for t, u, v in edges:
if t == 3:
if not ufa.unite(u, v):
ans += 1
else:
ufb.unite(u, v)
# 独占边
for t, u, v in edges:
if t == 1:
# Alice 独占边
if not ufa.unite(u, v):
ans += 1
elif t == 2:
# Bob 独占边
if not ufb.unite(u, v):
ans += 1
if ufa.setCount != 1 or ufb.setCount != 1:
return -1
return ans
java 解法, 执行用时: 13 ms, 内存消耗: 107.8 MB, 提交时间: 2023-09-21 10:35:21
class Solution {
public int maxNumEdgesToRemove(int n, int[][] edges) {
UnionFind ufa = new UnionFind(n);
UnionFind ufb = new UnionFind(n);
int ans = 0;
// 节点编号改为从 0 开始
for (int[] edge : edges) {
--edge[1];
--edge[2];
}
// 公共边
for (int[] edge : edges) {
if (edge[0] == 3) {
if (!ufa.unite(edge[1], edge[2])) {
++ans;
} else {
ufb.unite(edge[1], edge[2]);
}
}
}
// 独占边
for (int[] edge : edges) {
if (edge[0] == 1) {
// Alice 独占边
if (!ufa.unite(edge[1], edge[2])) {
++ans;
}
} else if (edge[0] == 2) {
// Bob 独占边
if (!ufb.unite(edge[1], edge[2])) {
++ans;
}
}
}
if (ufa.setCount != 1 || ufb.setCount != 1) {
return -1;
}
return ans;
}
}
// 并查集模板
class UnionFind {
int[] parent;
int[] size;
int n;
// 当前连通分量数目
int setCount;
public UnionFind(int n) {
this.n = n;
this.setCount = n;
this.parent = new int[n];
this.size = new int[n];
Arrays.fill(size, 1);
for (int i = 0; i < n; ++i) {
parent[i] = i;
}
}
public int findset(int x) {
return parent[x] == x ? x : (parent[x] = findset(parent[x]));
}
public boolean unite(int x, int y) {
x = findset(x);
y = findset(y);
if (x == y) {
return false;
}
if (size[x] < size[y]) {
int temp = x;
x = y;
y = temp;
}
parent[y] = x;
size[x] += size[y];
--setCount;
return true;
}
public boolean connected(int x, int y) {
x = findset(x);
y = findset(y);
return x == y;
}
}
cpp 解法, 执行用时: 412 ms, 内存消耗: 136 MB, 提交时间: 2023-09-21 10:35:03
// 并查集模板
class UnionFind {
public:
vector<int> parent;
vector<int> size;
int n;
// 当前连通分量数目
int setCount;
public:
UnionFind(int _n): n(_n), setCount(_n), parent(_n), size(_n, 1) {
iota(parent.begin(), parent.end(), 0);
}
int findset(int x) {
return parent[x] == x ? x : parent[x] = findset(parent[x]);
}
bool unite(int x, int y) {
x = findset(x);
y = findset(y);
if (x == y) {
return false;
}
if (size[x] < size[y]) {
swap(x, y);
}
parent[y] = x;
size[x] += size[y];
--setCount;
return true;
}
bool connected(int x, int y) {
x = findset(x);
y = findset(y);
return x == y;
}
};
class Solution {
public:
int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {
UnionFind ufa(n), ufb(n);
int ans = 0;
// 节点编号改为从 0 开始
for (auto& edge: edges) {
--edge[1];
--edge[2];
}
// 公共边
for (const auto& edge: edges) {
if (edge[0] == 3) {
if (!ufa.unite(edge[1], edge[2])) {
++ans;
}
else {
ufb.unite(edge[1], edge[2]);
}
}
}
// 独占边
for (const auto& edge: edges) {
if (edge[0] == 1) {
// Alice 独占边
if (!ufa.unite(edge[1], edge[2])) {
++ans;
}
}
else if (edge[0] == 2) {
// Bob 独占边
if (!ufb.unite(edge[1], edge[2])) {
++ans;
}
}
}
if (ufa.setCount != 1 || ufb.setCount != 1) {
return -1;
}
return ans;
}
};
java 解法, 执行用时: 15 ms, 内存消耗: 81.2 MB, 提交时间: 2023-09-21 10:34:19
class Solution {
public int maxNumEdgesToRemove(int n, int[][] edges) {
int count = 0;
UnionFind aliceUf = new UnionFind(n);
UnionFind bobUf = new UnionFind(n);
// 先连接所有的公共边
for (int[] edge : edges) {
if (edge[0] == 3) {
if (aliceUf.isConnected(edge[1], edge[2])) {
count++;
} else {
aliceUf.union(edge[1], edge[2]);
bobUf.union(edge[1], edge[2]);
}
}
}
// 再连接Alice边和Bob边
for (int[] edge : edges) {
if (edge[0] == 1) {
if (aliceUf.isConnected(edge[1], edge[2]))
count++;
else aliceUf.union(edge[1], edge[2]);
}
if (edge[0] == 2) {
if (bobUf.isConnected(edge[1], edge[2]))
count++;
else bobUf.union(edge[1], edge[2]);
}
}
return aliceUf.getSize() * bobUf.getSize() > 1 ? -1 : count;
}
static class UnionFind {
private final int[] father;
private int size;
public UnionFind(int n) {
this.father = new int[n + 1];
for (int i = 0; i <= n; i++)
father[i] = i;
this.size = n;
}
public int find(int i) {
if (father[i] == i)
return i;
else {
father[i] = find(father[i]);
return father[i];
}
}
public void union(int i, int j) {
father[find(i)] = find(j);
this.size -= 1;
}
public boolean isConnected(int i, int j) {
return find(i) == find(j);
}
public int getSize() {
return size;
}
}
}
python3 解法, 执行用时: 432 ms, 内存消耗: 54.3 MB, 提交时间: 2023-09-21 10:34:03
# 借助并查集按照人物遍历每一条边
class UnionFind:
def __init__(self,size):
self.father = [None] * (size+1)
self.num_of_sets = size
def find(self,x):
if self.father[x] is None: return x
self.father[x] = self.find(self.father[x])
return self.father[x]
def is_connected(self,x,y):
return self.find(x) == self.find(y)
def merge(self,x,y):
self.father[self.find(x)] = self.find(y)
self.num_of_sets -= 1
class Solution:
def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:
res = 0
uf_alice = UnionFind(n)
uf_bob = UnionFind(n)
for _type,n1,n2 in edges:
if _type == 3:
if not uf_alice.is_connected(n1,n2):
uf_alice.merge(n1,n2)
uf_bob.merge(n1,n2)
else:
res += 1
for _type,n1,n2 in edges:
if _type == 1:
if not uf_alice.is_connected(n1,n2):
uf_alice.merge(n1,n2)
else:
res += 1
if _type == 2:
if not uf_bob.is_connected(n1,n2):
uf_bob.merge(n1,n2)
else:
res += 1
return -1 if uf_alice.num_of_sets * uf_bob.num_of_sets > 1 else res