上次编辑到这里,代码来自缓存 点击恢复默认模板
class Solution {
public:
int minCost(int n, vector<int>& cuts) {
}
};
golang 解法, 执行用时: 5 ms, 内存消耗: 6.2 MB, 提交时间: 2024-11-11 00:07:42
func minCost(n int, cuts []int) int {
m := len(cuts)
cuts = append([]int{0}, cuts...)
cuts = append(cuts, n)
sort.Ints(cuts)
f := make([][]int, m + 2)
for i := range f {
f[i] = make([]int, m + 2)
}
for i := m; i >= 1; i-- {
for j := i; j <= m; j++ {
if i == j {
f[i][j] = 0
} else {
f[i][j] = int(^uint(0) >> 1)
}
for k := i; k <= j; k++ {
f[i][j] = min(f[i][j], f[i][k - 1] + f[k + 1][j])
}
f[i][j] += cuts[j + 1] - cuts[i - 1]
}
}
return f[1][m]
}
python3 解法, 执行用时: 696 ms, 内存消耗: 20.1 MB, 提交时间: 2023-09-20 11:38:04
class Solution:
def minCost(self, n: int, cuts: List[int]) -> int:
cuts.sort()
# 定义函数dfs(l, r): 表示将存在于区间[l, r]内的所有cuts中的元素完成切割
# 的最小花费,由于cuts所有元素均在[0, n]中,所以dfs(0, n)为最终答案
@cache
def dfs(l, r):
# 使用二分找到cuts中存在于区间[l, r]的元素范围
lo, hi = bisect_right(cuts, l), bisect_left(cuts, r)
# 若上下界相等则意味着区间[l, r]中不包含cuts中的任何元素
if lo == hi: return 0
# 计算本次花费
cost = r - l
# 枚举所有分割点,计算所有分割方案产生的花费,从中取得最小值即可
return cost + min(dfs(l, c) + dfs(c, r) for c in cuts[lo:hi])
return dfs(0, n)
#
def minCost2(self, n: int, cuts: List[int]) -> int:
cuts.sort()
f = cache(lambda l, r: min((r - l + f(l, c) + f(c, r) for c in cuts[bisect_right(cuts, l):bisect_left(cuts, r)]), default = 0))
return f(0, n)
cpp 解法, 执行用时: 64 ms, 内存消耗: 10.3 MB, 提交时间: 2023-09-20 11:37:03
class Solution {
public:
int minCost(int n, vector<int>& cuts) {
int m = cuts.size();
sort(cuts.begin(), cuts.end());
cuts.insert(cuts.begin(), 0);
cuts.push_back(n);
vector<vector<int>> f(m + 2, vector<int>(m + 2));
for (int i = m; i >= 1; --i) {
for (int j = i; j <= m; ++j) {
f[i][j] = (i == j ? 0 : INT_MAX);
for (int k = i; k <= j; ++k) {
f[i][j] = min(f[i][j], f[i][k - 1] + f[k + 1][j]);
}
f[i][j] += cuts[j + 1] - cuts[i - 1];
}
}
return f[1][m];
}
};
java 解法, 执行用时: 9 ms, 内存消耗: 40.2 MB, 提交时间: 2023-09-20 11:36:01
class Solution {
public int minCost(int n, int[] cuts) {
int m = cuts.length;
Arrays.sort(cuts);
int[] newCuts = new int[m + 2];
newCuts[0] = 0;
for (int i = 1; i <= m; ++i) {
newCuts[i] = cuts[i - 1];
}
newCuts[m + 1] = n;
int[][] f = new int[m + 2][m + 2];
for (int i = m; i >= 1; --i) {
for (int j = i; j <= m; ++j) {
f[i][j] = i == j ? 0 : Integer.MAX_VALUE;
for (int k = i; k <= j; ++k) {
f[i][j] = Math.min(f[i][j], f[i][k - 1] + f[k + 1][j]);
}
f[i][j] += newCuts[j + 1] - newCuts[i - 1];
}
}
return f[1][m];
}
}
python3 解法, 执行用时: 376 ms, 内存消耗: 16.2 MB, 提交时间: 2023-09-20 11:35:35
'''
我们用数组 cuts[1..m] 表示题目中给定的数组 cuts 按照升序排序后的结果,
其中 m 是数组 cuts 的长度,并令 cuts[0]=0,cuts[m+1]=n。
同时,我们用 f[i][j] 表示在当前待切割的木棍的左端点为 cuts[i−1],
右端点为 cuts[j+1] 时,将木棍全部切开的最小总成本。
'''
class Solution:
def minCost(self, n: int, cuts: List[int]) -> int:
m = len(cuts)
cuts = [0] + sorted(cuts) + [n]
f = [[0] * (m + 2) for _ in range(m + 2)]
for i in range(m, 0, -1):
for j in range(i, m + 1):
f[i][j] = 0 if i == j else \
min(f[i][k - 1] + f[k + 1][j] for k in range(i, j + 1))
f[i][j] += cuts[j + 1] - cuts[i - 1]
return f[1][m]
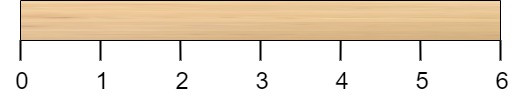
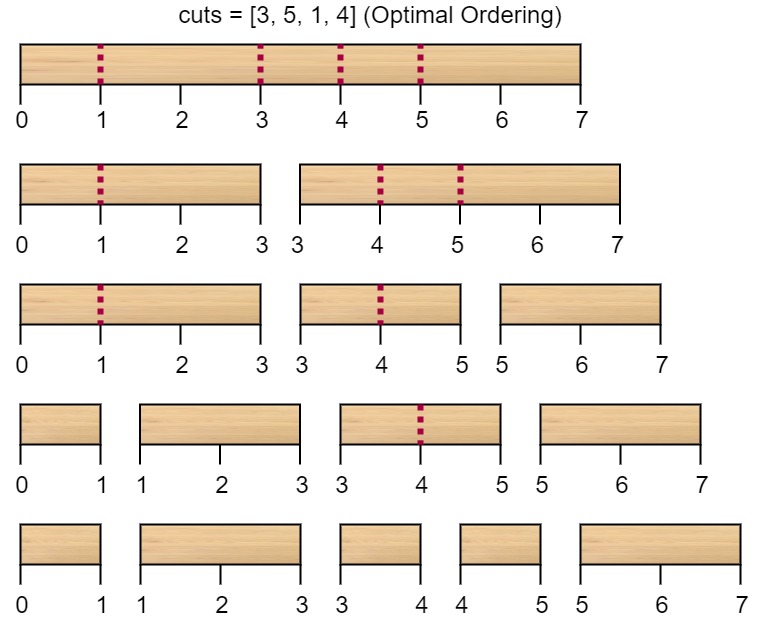
第一次切割长度为 7 的棍子,成本为 7 。第二次切割长度为 6 的棍子(即第一次切割得到的第二根棍子),第三次切割为长度 4 的棍子,最后切割长度为 3 的棍子。总成本为 7 + 6 + 4 + 3 = 20 。 而将切割顺序重新排列为 [3, 5, 1, 4] 后,总成本 = 16(如示例图中 7 + 4 + 3 + 2 = 16)。