参考答案:

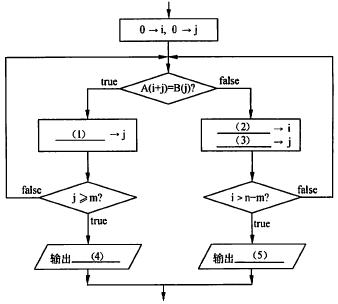
（1） j+l （2） i+1 （3） 0 （4） i （5）-1

详细解析:

本题采用的是最简单的字符子串查找算法。
　　在串A中查找是否含有串B，通常是在串A中从左到右取逐个子串与串B进行比较。在比较子串时，需要从左到右逐个字符进行比较。
　　题中已设串A的长度为n，存储数组为A，动态指针标记为i；串B的长度为m，存储数组为B，动态指针标记为j。
　　如果用伪代码来描述这种算法的核心思想，则可以用以下的两重循环来说明。
　　外循环为：
　　　For i=0 to n-m do
　　　　A(i)A(i+1）…A(i+m-1）~B(0）B（1）…B (m-1）
　　要实现上述比较，可以采用内循环：
　　　For j =0 to m-1 do
　　　　A(i+j)~B(j)
　　将这两重循环合并在一起就是：
　　　For i=0 to n-1 do
　　　For j=0 to m-1 do
　    　A(i+j)~B(j)
　　这两重循环都有一个特点：若发现比较的结果不相同时，就立即退出循环。因此，本题中的流程图可以间接使用循环概念。
　　初始时，i与j都赋值0，做比较A(i+j)~B(j)。
　　若发现相等，则继续内循环（走图的左侧）。j应该增1，继续比较，直到j=m为止，表示找到了子串（应输出子串的起始位置i）；若发现不等，则退出内循环，继续开始外循环（走图的右侧），j应恢复为0，i应增1，继续比较，直到i>n-m为止，表示不存在这样的子串（输出-1）。
　　在设计流程图时，主要的难点是确定循环的边界（何时开始，何时结束）。当难以确定边界值变量的正确性时，可以用具体的数值之例来验证。这是程序员应具备的基本素质。