参考答案:

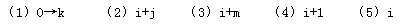
详细解析:

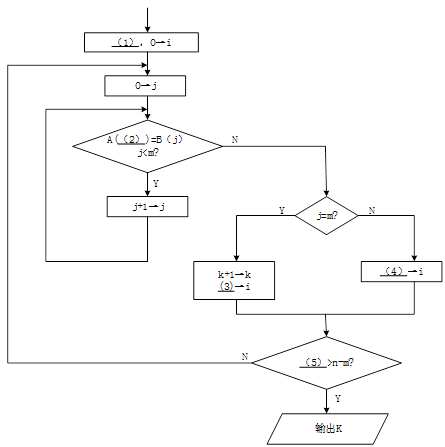
本题考查用流程图描述算法的能力。
在文章中查找某关键词出现的次数是经常碰的问题。例如，为了给文章建立搜索关键词，确定近期的流行语，迅速定位文章的某个待修改的段落，判断文章的用词风格，甚至判断后半本书是否与前半本书是同一作者所写（用词风格是否一致）等，都采用了这种方法。
流程图最终输出的计算结果 k就是文章字符串 A中出现关键词字符串 B的次数。显然，流程图开始时应将 k赋值 0，以后每找到一处出现该关键词，就执行增1操作 k=k+1。因此（1）处应填0→k。
字符串 A和 B的下标都是从 0开始的。所以在流程图执行的开始处，需要给它们赋值 0。接下来执行的第一个小循环就是判断 A(i)，A(i+1)，…，A(i+j一1)是否完全等于 B（0），B（1），…，B(m一1)，其循环变量j=0，l ，…，m-1。只要发现其中对应的字符有一个不相等时，该小循环就结束，不必再继续执行该循环。因此，该循环中继续执行的判断条件应该是 A（i+j）=B（j）且j<m。只要遇到 A（i+j）≠B（j）或者 j=m（关键词各字符都已判断过）就不再继续执行该循环了。因此流程图的（2）处应填i+j。
许多考生在（2）处填 i，当j 增 1 变化后，仍然使用 A（i）进行比较就不对了。因此，在检查循环程序段时应多走查一次循环。
如果（2）处整体的判断条件不成立，则该判断关键词的小循环结束。此时可能有两种情况。一是在 j=0，1 ，…，m-1 时全都成立 A（i+j）=B（j）（找到了一处关键词），直到j=m 时才结束小循环；二是在 j<m 时就发现了字符不等的情况，这说明此处并不出现关键词。 因此流程图中用 j<m来区分找到与没有找到关键词的两种情况。
对于 j=m，己找到一处关键词的情况，显然应该执行 k=k+1，对关键词出现次数的变量 k进行增 1计算。同时，为了继续进行以后的判断，应将字符串  A 的下标 i右移 m（这是因为题中假设关键词的出现不允许重叠）。因此（3）处应填写 i+m，表示应该从已出现的关键词后面开始再继续进行判断。由于此时的   j=m，书写i+j的答案也是正确的，但这不是程序员的好习惯，因为这不符合逻辑思维的顺势，在程序不断修改的过程中容易出错。不少考生在（3）处填写i+1，这意味着下次判断关键词将从A（i+1）开始，这就 使关键词的出现有可能发生部分重叠的现象。
流程图中，对于 j<m 的情况，表示刚才判断关键词时并非各个字符都完全相同，也就是说，刚才的判断结论是此处并没有出现关键词。即 A（i）开始的子串并不是关键词。因此，下次判断关键词应该以 A（i+1）开始，即（4）处应填 i+1。
在下次判断关键词之前还应该判断是否全文已经判断完。最后一次小循环判断应该是对 A（n-m），A（n-m+1），… ，A（n一1）的判断。下标 n-m来自从 n-1 倒数 m个数。可以先试验写出A（n-m），A（n-m+1），… ，A（n一1），再判断其个数是否为m。经检查，个数为 （n-1）-（n-m）+1=m个，所以这是正确的。也可以用例子来检查次数是否正确。检查次数是程序员的基本功，数目的计算很容易少一个或多一个。 既然最后一次判断关键词应该是对A（n-m），A（n-m+1），… ，A（n一1）的判断，即对 i=n-m进行的小循环判断，所以当 i>n-m 时就应该停止大循环，停止再查找关键词了。