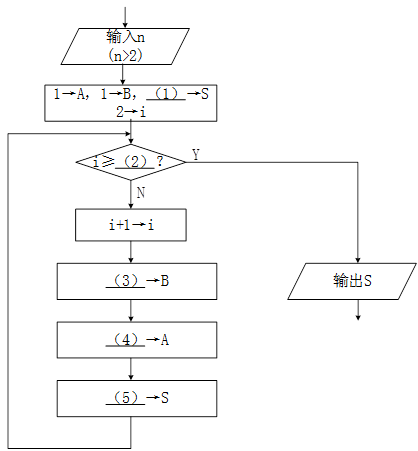
参考答案: (1)2或 A+B  (2) n   (3)A+B  (4) B-A (5) S+B

详细解析:

菲波那契数列的特点是首 2 项都是1，从第 3 项开始，每一项都是前两项之和。该数列的前几项为1， 1， 2 ，3，5，8，...。
在流程图中，送初始值 1→A ，1→B 后，显然前2项的和 S 应等于2，所以(1)处应填 2 (或 A+B) 。此时2→i (i 表示动态的项编号)，说明已经计算出前2项之和。接着判断循环的结束条件。显然当1=n时表示已经计算出前 n 项之和，循环可以结束了。 因此(2)处填n。判断框中用">"或"≤"的效果是一样的，因为随着i的逐步增 1， 只要有 i=n结束条件，就不会遇到 i>n 的情况。不过编程的习惯使循环结束条件扩大些， 以防止逻辑出错时继续循环。
接下来 i+l →i 表示数列当前项的编号增1，继续往下计算。原来的前两项值(分别在变量 A 和 B 中)将变更成新的前两项再放到变量 A 和 B 中。

首先可以用 A+B→B 实现（原A) + (原B) →(新 B) ，因此(3)处填A+B 。为了填新 A 值(原来的B值)，不能用 B→A，因为变量B的内容已经改变为(原A)+(原B) ，而B-A 正是((原A) + (原B)) - (原A)  = (原B) ，因此可以用B-A→A 来实现新 A 的赋值。这样，(4) 处填 B-A 。最后应是前n项和值的累加（比原来的S值增加了新B值)，所以 (5) 处应填S+B。填完各个空后，最好再用具体的数值来模拟流程图走几个循环检查所填的结果(这是防止逻辑上出错的好办法)。