（）（15分，每空3分）
【说明】
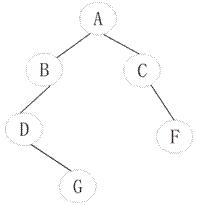
　　一棵非空二叉树中“最左下”结点定义为：若树根的左子树为空，则树根为“最左下”结点；否则，从树根的左子树根出发，沿结点的左孩子分支向下查找，直到某个结点不存在左孩子时为止，该结点即为此二叉树的“最左下”结点。例如：下图所示的以A为根的二叉树的“最左下”结点为D，以C为根的子二叉树中的“最左下”结点为C。二叉树的结点类型定义如下：
　　typedef struct BSTNode {
　　　int data ;
　　　struct BSTNode *lch ， *rch; //结点的左、右孩子指针
　} *BSTree;

　　函数BSTree Find_Del (BSTree root )的功能是：若root指向一棵二茶树的根结点，则找出该结点的右子树上的“最左下”结点 *p，并从树中删除以 *p为根的子树，函数返回被删除子树的根结点指针；若该树根的右子树上不存在“最左下”结点，则返回空指针。
【函数】
　　BSTree Find_Del (BSTree root)
　{ 　BSTree p， pre;
　　　If ( !root ) return NULL; /* root 指向的二叉树为空树 */
　　　　　___（1）___ ; /* 令p指向根结点的右子树 */
　　　if ( !p ) return NULL;
　　　　　___（2）___ ; /* 设置 pre 的初值 */
　　　while ( p -> lch ) { /* 查找“最左下”结点 */
　　　　　pre = p ; p = __（3）__ ;
　　}
　　　if ( __（4）__ = = root ) /* root的右子树根为“最左下”结点*/
　　　　　pre -> rch =NULL;
　　　else
　　　　　__（5）__ = NULL; /* 删除以“最左下”结点为根的子树*/
　　　return p;
　}

（）（15分，每空3分）
【说明】
　　一棵非空二叉树中“最左下”结点定义为：若树根的左子树为空，则树根为“最左下”结点；否则，从树根的左子树根出发，沿结点的左孩子分支向下查找，直到某个结点不存在左孩子时为止，该结点即为此二叉树的“最左下”结点。例如：下图所示的以A为根的二叉树的“最左下”结点为D，以C为根的子二叉树中的“最左下”结点为C。二叉树的结点类型定义如下：
　　typedef struct BSTNode {
　　　int data ;
　　　struct BSTNode *lch ， *rch; //结点的左、右孩子指针
　} *BSTree;

　　函数BSTree Find_Del (BSTree root )的功能是：若root指向一棵二茶树的根结点，则找出该结点的右子树上的“最左下”结点 *p，并从树中删除以 *p为根的子树，函数返回被删除子树的根结点指针；若该树根的右子树上不存在“最左下”结点，则返回空指针。
【函数】
　　BSTree Find_Del (BSTree root)
　{ 　BSTree p， pre;
　　　If ( !root ) return NULL; /* root 指向的二叉树为空树 */
　　　　　___（1）___ ; /* 令p指向根结点的右子树 */
　　　if ( !p ) return NULL;
　　　　　___（2）___ ; /* 设置 pre 的初值 */
　　　while ( p -> lch ) { /* 查找“最左下”结点 */
　　　　　pre = p ; p = __（3）__ ;
　　}
　　　if ( __（4）__ = = root ) /* root的右子树根为“最左下”结点*/
　　　　　pre -> rch =NULL;
　　　else
　　　　　__（5）__ = NULL; /* 删除以“最左下”结点为根的子树*/
　　　return p;
　}