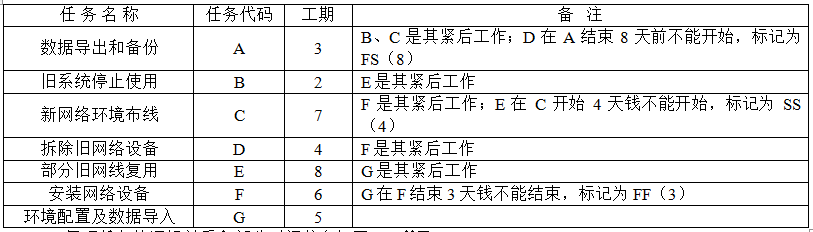
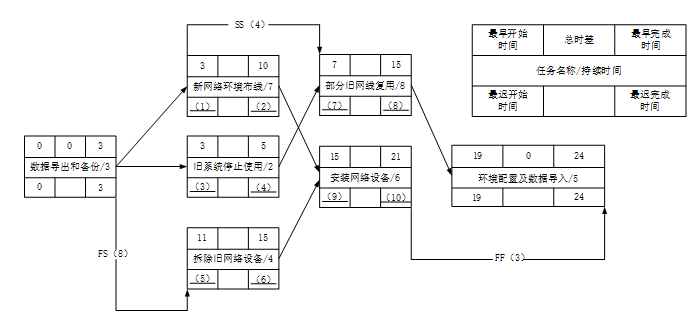
参考答案:

【问题1】
（1）7
（2）14
（3）9
（4）11
（5）11
（6）15
（7）11
（8）19
（9）15
（10）21
【问题2】
（11）6
（12）4
（13）4
【问题3】
（14）D
（15）F

详细解析:

本题考查项目管理中网络图、关键路径及相关计算。
项目计划网络图中时间参数的计算应在确定各项工作的持续时间之后进行。
1．最早开始和最早完成时间ES、EF。
计划网络图中各项工作的最早开始时间和最早完成时间的计算应从网络计划的起始结点开始，顺着箭线方向依次逐项计算。
（1）起始结点的最早开始时间为零。
（2）工作的最早开始时间等于该工作的各个紧前工作的最早完成时间的最大值，即ES=max{紧前工作的EF}。
（3）工作的最早完成时间等于该工作的最早开始时间加上其持续时间，即EF=ES+本工作持续时间。
2．最迟开始时间和最迟完成时间LS、LF。
网络计划中各项工作的最迟开始时间和最迟完成时间的计算应以项目规定或计算的工期为基准，从网络计划的终止结点，逆着箭线方向依次逐项计算。
（1）最迟结束时间：某工作的最迟结束时间等于该工作的各项紧后工作的最迟开始时间的最小值，即LF=min{紧后工作的LS}。
（2）最迟开始时间：本项工作的最迟结束时间减本项工作的持续时间，即LS=LF-工作的持续时间。
3．工作的总时差TF：工作的总时差指在不影响整个项目最早完成时间的前提下，各项工作的完工期可以推延的时间。工作总时差等于该工作最迟完成时间与最早完成时间之差，或该工作最迟开始时间与最早开始时间之差，即TF=LF-EF，或TF=LS-ES。
4．工作的自由时差FF：工作自由时差指在不影响紧后工作的最早开始时间的前提下，一项工作的完工期可以推延的时间。自由时差的计算应按以下两种情况分别考虑：
（1）对于有紧后工作的工作，其自由时差等于本工作之紧后工作最早开始时间减本工作最早完成时间所得之差的最小值，即FF=min{ES（紧后工作）}-EF。
（2）对于无紧后工作的工作，也就是以网络计划终点结点为完成结点的工作，其自由时差等于计划工期与本工作最早完成时间之差。
需要指出的是，对于网络中以终点结点为完成结点的工作，其自由时差与总时差相等。此外，由于工作的自由时差是其总时差的构成部分，所以，当工作的总时差为零时，其自由时差必然为零，可不必进行专门计算。
在实际项目中，可能会出现其他情况。例如，紧后工作和紧前工作具有一定的平行特性，即紧后工作的开始并不以紧前工作的结束为前提，紧后工作只需在紧前工作开始一段时间后即可开始，将这样工作间的平行关系称为搭接关系。一般将这样的搭接关系分成四类：
（1）结束——开始型（finish-to-start）：B在A结束T时间之前不能开始，标记为FS（T）如下图（a）所示。
（2）结束——结束型（finish-to-finish，FF）：B在A结束T时间之前不能结束，标记为FF（T）如下图（b）所示。
（3）开始——开始型（start-to-start，SS）：B在A开始T时间之前不能开始，标记为SS（T）如下图（c）所示。
（4）开始——结束型（start-to-finish，SF）：B在A开始T时间之前不能结束，标记为SF（T）如下图（d）所示。 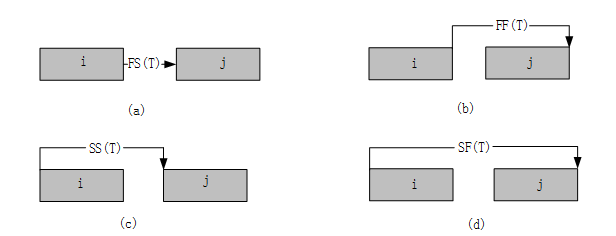  具体计算如下：

（1）结束——开始型（finish-to-start，FS（T））：B在A结束T时间之前不能开始，标记为FS（T），T表示时间间隔，各参数计算规则如下：
最早时间：ESj=EFi+FS（T）
最迟时间：LFi=LSj-FS（T）
自由时差：FFi=ESj-FS（T）-EFi
（2）结束——结束型（FF）：B在A结束T时间之前不能结束，标记为FS（T），T表示时间间隔，各参数计算规则如下：
最早时间：EFj=EFi+FF（T）
最迟时间：LFi=LFj-FF（T）
自由时差；FFi=EFj-FF（T）-EFi
（3）开始——开始型（SS）：B在A开始T时间之前不能开始，标记为FS（T），T表示时间间隔，各参数计算规则如下：
最早时间：ESj=ESi+SS（T）
最迟时间：LSi=LSj-SS（T）
自由时差：FFi=ESj-SS（T）-ESi
（4）开始——结束型（SF）：B在A开始T时间之前不能结束，标记为FS（T），T表示时间间隔，各参数计算规则如下：
最早时间：EFj=ESi+SF（T）
最迟时间：LSi=LFj-SF（T）
自由时差：FFi=EFj-SF（T）-ESi
这四类情况下，总时差的计算规则与一般网络相同。
根据上述公式，问题1计算结果如下：

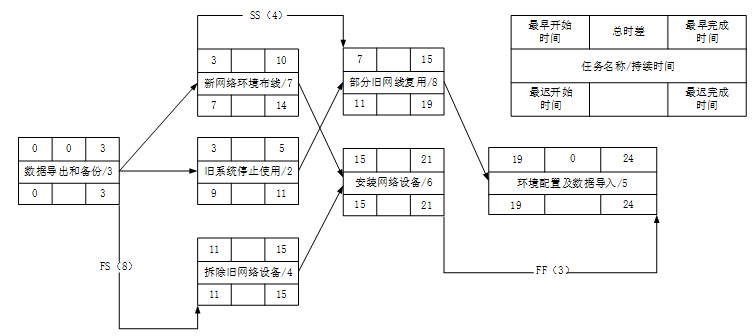
问题2计算结果如下：

问题3计算结果如下：
总时差最小的工作为关键工作，由关键工作构成的线路为关键线路或关键路径。本项目中从开始结点到最终结点，A、D、F、G工作的总时差均为0，故本项目的关键路径是A-D-F-G。