参考答案:

【问题1】
（1）7
（2）8
（3）6
（4）A
（5）A
（6）F，G或G，F
【问题2】
（7）C/7
（8）E/8
（9）F/8
（10）G/4
（11）A，C，F，H或1，2，4，3，7，9
（12）29或29天
【问题3】
（13）4
（14）0
（15）19
（16）15
（17） 3
（18） 0

详细解析:

试题四分析
本题考查项目控制方法应用、优化与计算，考查知识点主要有甘特图画法，单代号网络图和双代号网路图进行项目控制优化的使用，关键路线寻找方法等。
[问题1]
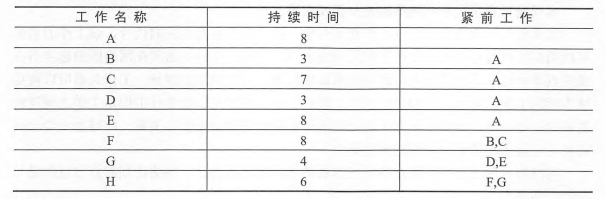
甘特图可用来安排项目中各项工作的进度，同时还能和各项资源在不同阶段的需求数量结合，有利于对项目管理过程进行有效的控制，当项目中某些工作进度安排有机动时间时，可以利用机动时间安排工作的实施进度，使项目对资源的集中需求尽可能分散，得到合理利用。由甘特图可填写项目的任务如下表所示，反之亦然。

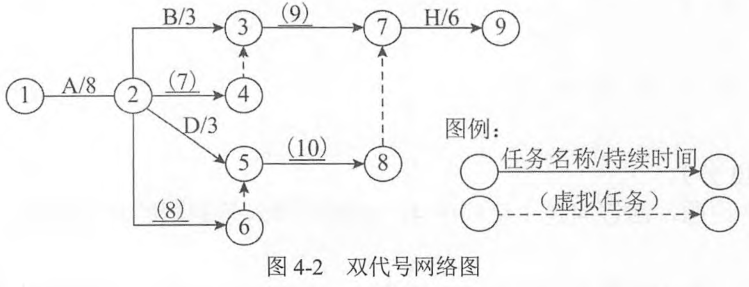
双代号网络图又称箭线式网络图，它是以箭线及其两端节点的编号表示工作，同时，节点表示工作的开始或结束以及工作之间的连接状态。网络图中的节点都必须有编号，应使每一条箭线上箭尾节点编号小于箭头节点编号。在双代号网络图中，- -项工作必须有唯一的一条箭线和相应的一 对不重 复出现的箭尾、箭头节点编号。因此，一项工作的名称可以用其箭尾和箭头节点编号来表示。可以允许存在虚箭线，虛箭线不代表实际工作，我们称之为虚工作。虚工作既不消耗时间，也不消耗资源。虚工作主要用来表示相邻两项工作之间的逻辑关系。但有时为了避免两项同时开始、同时进行的工作具有相同的开始节点和完成节点，也需要用虚工作加以区分。根据甘特图和项目任务分解图绘制的双代号图如右图所示。

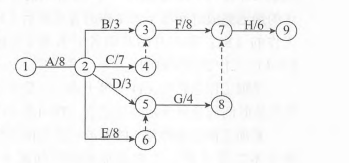
[问题3]
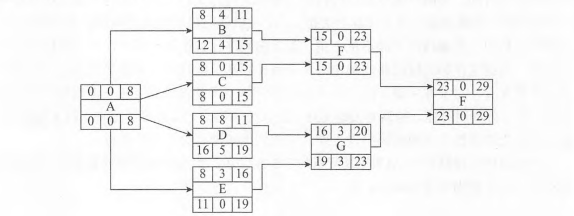
本问题考查由网络图计算关键路线。关键线路上所有工作的持续时间总和称为该线路的总持续时间，将网络图中所有线路的作业时间进行比较，总持续时间最长的线路称为关键线路，关键线路上的工作称为关键工作，关键线路的长度就是网络计划的总工期。在网络计划中，关键线路可能不止一 条，而且在网络计划执行过程中，关键线路还会发生转移。关键工作和关键线路的确定对于项目计划和控制具有十分重要的意义。从整个项目管理来看，对于非关键工序，由于总存在时差，所以它的进度在- -定范围内可自由安排，或充分利用时差，抽调非关键工序上的人力、物力、设备等资源来支持关键线路，保证关键线路提前完工或起码不误工期，以达到缩短项目总工期的目标。该项目的关键路径为ACFH或节点为1-2-4-3-7-9,此为持续时间最长路径，即为关键路径。总工期为8+7+8+6-29天。

[问题4]
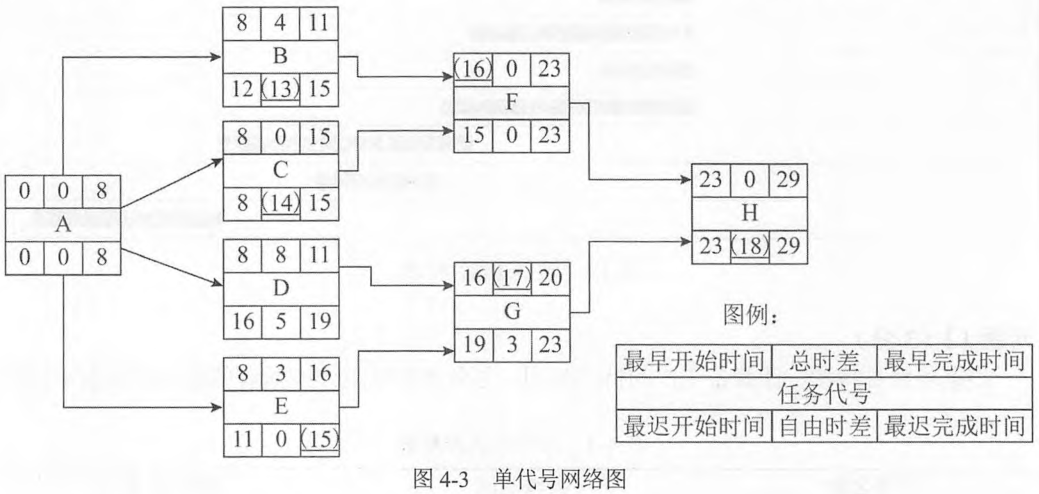
本问题考查单代号网络图相关知识及应用。在单代号网络图中，一项工作必须有唯- -的一一个节点及相应的代号，该工作的名称可以用其节点编号来表示。在单代号网络图中，虚拟工作只能出现在网络图的起点节点或终点节点处。工作之间先后顺序关系是项目逻辑关系的组成部分。工作关系可以被描述为紧前工作、紧后工作和平行工作。紧前工作、紧后工作及平行工作是工作之间逻辑关系的具体表现，只要能根据工作之间的关系明确其紧前或紧后关系，即可据此绘出网络图。它是正确绘制网络图的前提条件。

网络参数的计算应在确定各项工作的持续时间之后进行，网络计划起点节点的最早开始时间为零。

网络计划中各项工作的最早开始时间(ES)和最早完成时间(EF)的计算应从网络计划的起点节点开始，顺着箭线方向依次逐项计算。工作的最早开始时间等于该工作的各个紧前工作的最早完成时间的最大值，ES= max {紧前工作的EF};工作的最早完成时间等于该工作的最早开始时间加上其持续时间，EF-ES+本工作 持续时间。

网络计划中各项工作的最迟开始时间(LS)和最迟完成时间(LF) 的计算应以项目规定或计算的工期为基准，从网络计划的终止节点，逆着箭线方向依次逐项计算。某工作的最迟完成时间等于该工作的各项紧后工作的最迟开始时间的最小值，LF=min{紧后工作的LS};最迟开始时间等于本项工作的最迟完成时间减本项工作的持续时间，LS=LF-工作的持续时间。

某项工作总时差(TF)等于该工作最迟完成时间与最早完成时间之差，或该工作最迟开始时间与最早开始时间之差，TF=LF-EF 或TF=LS _ES。

某项工作自由时差(FF) 的计算有两种情况，对于有紧后工作的工作，其自由时差等于本工作之紧后工作最早开始时间减本工作最早完成时间所得之差的最小值，FF-min{ES (紧后工作) }- EF;对于无紧后工作的工作，也就是以网络计划终点节点为完成节点的工作，其自由时差等于计划工期与本工作最早完成时间之差。