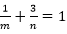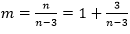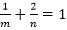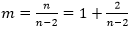参考答案: D
详细解析:
本题考查的是代数方程求解。
方法一:对于条件一,已知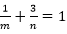
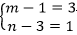
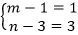
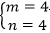
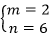
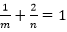
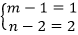
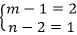
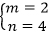
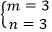
方法二:对于条件一,已知
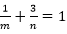
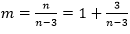
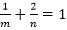
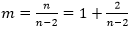
设m,n是正整数,则能确定m+n。
(1)1/m+3/n=1。(2)1/m+2/n=1
A. 条件(1)充分,但条件(2)不充分。
B. 条件(2)充分,但条件(1)不充分。
C. 条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来充分。
D. 条件(1)充分,条件(2)也充分。
E. 条件(1)和(2)单独都不充分,但条件(1)和条件(2)联合起来也不充分。
参考答案: D
详细解析:
本题考查的是代数方程求解。
方法一:对于条件一,已知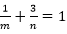
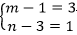
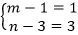
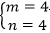
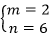
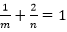
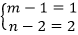
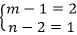
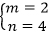
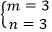
方法二:对于条件一,已知