参考答案:
【问题1】(共9分,各3分)
(1)nv[i-1][j]≥nv[i-1][j-p[i]]+v[i]
(2)nv[i][j]=nv[i-1][j]
(3)j=j-p[i]
【问题2】(共4分,各2分)
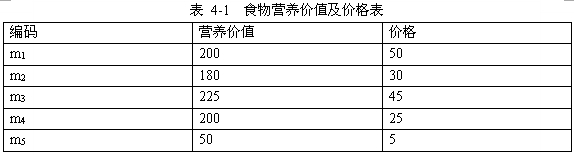
(4)m2,m3,m4(注:答案中食物编码无前后顺序关系)
(5)605
【问题3】(共2分)
(6)O(nM),或O(n×M),或O(n*M)
详细解析: