参考答案:
【问题1】
(2)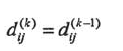
(3)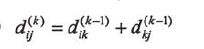
(4)
(5)min_v=1
(6)min_v
【问题2】
(7)O(n3)
详细解析:
本题考查的是算法的设计和分析技术。
【问题1】
本问题考查算法流程。第(1)空表示主循环,k是循环控制变量,故第(1)空填k=1 to n。第(2)和(3)空根据题意和递归式,可分别得到答案为 和
和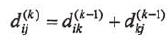 。计算了任意两个顶点之间的最短路径之后,对每个顶点,开始统计其到所有其他顶点的最短路径之和,因此第(4)空填
。计算了任意两个顶点之间的最短路径之后,对每个顶点,开始统计其到所有其他顶点的最短路径之和,因此第(4)空填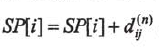 。第13和第14行初始化,假设最小的到所有其他顶点的最短路径之和为第一个顶点的最小路径之和,大型超市的最佳位置为第一个顶点,故第(5)空填min_v = 1。最后要求返回大型超市的最佳位置,即到所有其他项点的最短路径之和最小的顶点,故第(6)空填min_v。
。第13和第14行初始化,假设最小的到所有其他顶点的最短路径之和为第一个顶点的最小路径之和,大型超市的最佳位置为第一个顶点,故第(5)空填min_v = 1。最后要求返回大型超市的最佳位置,即到所有其他项点的最短路径之和最小的顶点,故第(6)空填min_v。
【问题2】
本问题考查【问题1】中的伪代码第2~8行,计算任意两点之间的最短路径,有三重循环,故时间复杂度为O(n3)。第9~12行,计算每个点到任意其他点的最短路径之和,有两重循环,故时间复杂度为O(n2)。第15~18行,在所有点的最短路径之和中找到最小的最短路径之和,时间复杂度为O(n)。故算法总的时间复杂度为O(n3)。


