参考答案: C B

详细解析:

本题考查数据结构基础知识。
　　遍历运算是二叉树的基本运算，主要有先序、中序、后序和层序遍历。
　　先序遍历的基本方法：对于非空二叉树，先访问根结点，然后先序遍历根的左子树，最后先序遍历根的右子树。因此，若已知某二叉树的先序遍历序列，则可直接得到其树根结点。
　　中序遍历的基本方法：对于非空二叉树，先中序遍历根的左子树，然后访问根结点，最后中序遍历根的右子树。因此，若已知某二叉树的根结点，则一可根据中序遍历序列将该二叉树左右子树上的结点划分开。
　　后序遍历的基本方法：对于非空二叉树，首先后序遍历根的左子树，接着后序遍历根的右子树，最后访问根结点。因此，若已知某二叉树的后序遍历序列，则可直接得到其树根结点。
　　题中给出的先序遍历序列为①、②、③、④、⑤，可知树根结点是①，据此再结合中序遍历序列②、①、④、③、⑤，可知②是根结点①左子树上的结点，由于是左子树上唯一的一个结点，因此②是根结点①的左孩子。对于右子树上的结点④、③、⑤，因右子树的先序遍历序列为③、④、⑤，因此③是根结点①的右孩子。依此类推，可知④是结点③的左孩子，⑤是结点③的右孩子。该二叉树如下图所示。

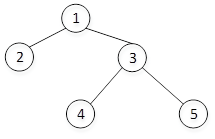
　　从二叉树的遍历过程可知，从先序遍历序列和后序遍历序列中无法将左子树和右子树上的结点区分开，因此，由某棵二叉树的先序遍历序列和后序遍历序列不能构造出该二叉树的中序遍历序列。
　　层序遍历二叉树的方法：设二叉树的根结点所在层数为1，则层序遍历二叉树的操作定义为从树的根结点出发，首先访问第一层的结点（根结点），然后从左到右依次访问第二层上的结点，接着是第三层上的结点，依此类推，自上而下、自左至右逐层访问树中各层上的结点。