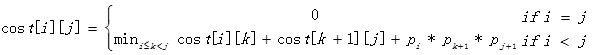参考答案:

详细解析:

在解答本题时，需要注意的第一个问题便是矩阵的乘法到底是怎么进行的。

       一个n行m列的矩阵可以乘以一个m行p列的矩阵，得到的结果是一个n行p列的矩阵，其中的第i行第j列位置上的数等于前一个矩阵第i行上的m个数与后一个矩阵第j列上的m个数对应相乘后所有m个乘积的和。如：

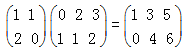
    在本题中，题干部分提到“发现矩阵链乘问题具有最优子结构”，这是利用动态规划法求解最优解问题的典型特征。所以（5）应填动态规划法。

    接下来分析（1）-（4）空，这几个空中，最容易回答的是（3）和（4）。（3）空可通过题目给出的递归式分析得到，其中cost数组部分与公式完全一致，而p数组在程序中是seq，所以回答时修正即可，（3）填：cost[i][k]+cost[k+1][j]+seq[i]*seq[k+1]*seq[j+1]。第（4）空的上一句为：tempCost = temp，即保存当前状态最优解，由于在保存最优解时，不仅涉及cost的记录，还涉及其位置k的记录，所以需要在此进行tempTrace=k的操作。

       （1）与（2）相对复杂，其中（1）是对i值范围的确定，而（2）是对j的赋值操作（由于后面用到了j，但程序中没有对j的赋值，从而断定该空是对j的赋值）。两者一并起到一个效果，对cost数组操作时的操作范围与顺序。由于在进行矩阵链乘操作时，分析解空间所用到的是cost右上角的三角矩阵，而操作时，是对这个三角矩阵从左至右，呈斜线的访问（如图所示）。所以（1）和（2）分别填i<n-p和j=i+p。

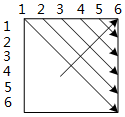
    该程序由于涉及3重循环，所以时间复杂度为：O（n³）。通过手动运行程序的方式可知最优解为：

       （A1A2）（（A3A4）（A5A6））。

       总计算次数为2010。