参考答案: D

详细解析:

本题考查栈的相关问题。
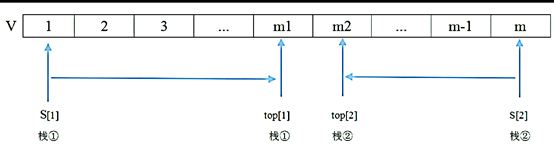
由题干描述可知，现有两栈共享空间V[1..n]， top[i]代表i( i=1,2)个栈的栈顶(两个栈都空时top[1]= 1、top[2]= n)，栈1的底在V[1]，栈2的底在V[n]。
若按照顺序从底到上从V【1】到V【n】都将存入栈内，这个栈共享空间V【1.....n】，可知该栈一分为二，栈1可以是开口向上，底为V【1】，栈2是开口向上，底为V【n】，要使栈满，就需要保持两个栈重合，即两个栈的开口位置相邻，有top【1】-top【2】==1，如下图所示：