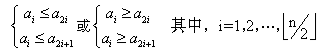列表

详情

阅读下列说明和C代码，回答问题1至问题3，将解答写在答题纸的对应栏内。
【说明】
堆数据结构定义如下：
对于n个元素的关键字序列{a1，a2，...,an}，当且仅当满足下列关系时称其为堆。

在一个堆中，若堆顶元素为最大元素，则称为大顶堆；若顶堆元素为最小元素，则称为小顶堆。堆常用完全二叉树表示，图4-1是一个大顶堆的例子。

图4-1  大顶堆示例
堆数据结构常用于优先队列中，以维护由一组元素构成的集合。对应于两类堆结构，优先队列也有最大优先队列和最小优先队列，其中最大优先队列采用大顶堆，最小优先队列采用小顶堆。以下考虑最大优先队列。
假设现已建好大顶堆A，且已经实现了调整堆的函数heapify（A,n,index）。
下面将C代码中需要完善的三个函数说明如下：
（1）heapMaximum(A)：返回大顶堆A中的最大元素。
（2）heapExtractMax(A)：去掉并返回大顶堆A的最大元素，将最后一个元素“提前”到堆顶位置，并将剩余元素调整成大顶堆。
（3）maxHeapInsert(A,key)：把元素key插入到大顶堆A的最后位置，再将A调整成大顶堆。
优先队列采用顺序存储方式，其存储结构定义如下：
#define PARENT(i)   i/2
typedef struct array{
int   *int_array;  //优先队列的存储空间首地址
int    array_size;  //优先队列的长度
int    capacity;  //优先队列存储空间的容量
}ARRAY;

 

 【C代码】

（1）函数heapMaximum
int heapMaximum(ARRAY  *A){  return  (1)  ;  }
（2）函数heapExtractMax
int heapExtractMax(ARRAY *A){
int max;
max=A->int_array[0];
（2）;
A->array_size --;
heapify(A,A->array_size,0);  //将剩余元素调整成大顶堆
return max;
}
（3）函数maxHeapInsert
int maxHeapInsert(ARRAY *A,int key){
int  i,*p;
if  (A->array_size == A->capacity)    {  //存储空间的容量不够时扩充空间
p=(int*)realloc(A->int_array,A->capacity *2 * sizeof(int));
if (!p) return -1;
A->int_array = p;
A->capacity = 2 * A->capacity;
}
A->array_size ++;
i = （3） ;
while (i > 0 && （4）){
A->int_array[i] = A->int_array[PARENT(i)];
i = PARENT(i);
}
（5）;
return 0;
}

【问题1】（10分）
       根据以上说明和C代码，填充C代码的空（1）~（5）。

【问题2】（3分）
       根据以上C代码，函数heapMaximum、heapExtractMax和maxHeapInsert的时间复杂度的紧致上界分别为 （6） 、（7） 、（8） （用O符号表示）。

【问题3】（2分）
       若将元素10插入到堆A={15，13，9，5，12，8，7，4，0，6，2，1}中，调用maxHeapInsert函数进行操作，则新插入的元素在堆A中的第 （9） 个位置（从1开始）。


参考答案: 【问题1】
（1）A->int_array[0]
（2）A->int_array[0]= A->int_array[A->array_size-1]
（3）A-> array_size-1
（4）A->int_array[PARENT(i)]<key
（5）A->int_array[i]=key
【问题2】
（6）O(1)   （7）O(lgn)    （8）O(lgn)
【问题3】
（9）3

 

详细解析:

【问题1】
    本题考查堆数据结构的相关内容。题目告诉我们函数heapMaximum（A）的功能返回大顶堆A中的最大元素；函数heapExtractMax（A）的功能是去掉并返回大顶堆A的最大元素，将最后一个元素“提前”到堆顶位置，并将剩余元素调整成大顶堆；而函数maxHeaplnsert（A， key）的功能是把元素key插入到大顶堆A的最后位置，再将A调整成大顶堆。
第（1）空在函数heapMaximum（A）中，而且从程序中可以看出，是返回的结果，那么应该是大顶堆中最大元素，就应该是A->int_array[0]。
第（2）空在函数heapExtractMax（A）中，根据该函数的功能描述，并结合程序可以看出，第（2）空是在将最大元素移出后，那么接下了来应该处理将最后一个元素“提前”到堆顶位置，那么就应该是A->int_array[0] = A->int_array[A->array_size -1]。
第（3）（4）（5）空都在函数maxHeaplnsert（A， key）中。从程序和函数的功能我们可以知道，从程序第（3）空最后，其作用是找到元素key的插入位置并插入该元素。第（3）空是给变量i赋值，从后面的程序中我们可以看出i是做为数组下标的；而查找元素插入的位置应该从后往前的顺序，因此i的初值应该为A->array_size – 1，从循环中也可以看出i的值在逐渐变小。
第（4）空是循环的一个条件，而循环的作用是找到合适的插入位置，由于大顶堆的特点是根节点的值大于左右子树节点上的值，那么找到比待插入元素大的父节点时，应该就找到了它插入的合适位置，而每次操作后i的值被赋值为PARENT（i），很显然这是找到其父节点的存储位置，因此循环结束的一个条件就是找到一个比key值大的父节点，那么循环继续的条件就是父节点的值小于key的值，所以本空的答案为A->int_array[PARENT(i)]<key 。第（5）空就是插入元素，所以应该填A->int_array[i] = key。
【问题2】
    根据题目描述，heapMaximum用来返回大顶堆A中的最大元素，而且大顶堆已经建成，只需要通过一步操作就能取到。因此时间复杂度是O（1），
    而对于heapExtractMax是用来去掉大顶堆A的根，然后重新建堆，当输出堆顶结点并将堆中最后一个结点设置为根结点之后，根结点将有可能不再满足堆的性质，所幸的是整个序列也只有根结点一处的堆结构可能被破坏，其余结点仍然满足堆性质，故可利用性质进行堆调整，算法的基本思想为：将新堆顶沿着其关键字较大的孩子结点向下移动，直到叶子结点或者满足堆性质为止。因此相对于有N个元素的堆，只需要log2n次比较即可完成，因此时间复杂度是O（log2n），这与书本说堆排序的算法时间复杂度是：O(nlog2n)不冲突，因为书本上是对堆中所有元素进行操作，而这里其实相当于只将一个元素入堆，因此少了一个n。同样的道理可以得到maxHeaplnsert的时间复杂度O（log2n）。
【问题3】
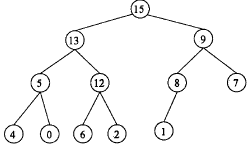
这个我们可以结合题目给出的那个大顶堆的图来看，首先将key插入在最后，应该是8这个节点的右子树，由于10比8大，所以应该互换，再与节点9比较，由于10仍然大于9，所以也应该互换，这个时候再与其父节点15比较，由于小于15，所以不需要再调整，那么调整后的结果就是10这个元素应该作为根节点15的右子树。那么很显然10应该是在堆A中第3个位置。

上一题

© 2024 educity.cn