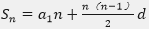参考答案: D
详细解析:
答案:D
【考点判断】 等差数列求和公式
【解题必知】
①等差数列求和公式:
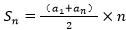
②等差数列下标和定理:在等差数列{an}中,若k+l=m+n,则ak+al=am+an
③等差数列求公差公式: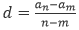
等差数列通项公式:an=a1+(n-1)d 或 an=am+(n-m)d
【解题思路】 分别求出S10与S3的值,两者之差即为所求。
【解题步骤】
由等差数列下标和定理:a5+a6=a1+a10=3-2=1
所以: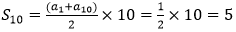
根据公差公式,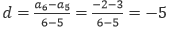
所以通项为:an=a5+(n-5)d=3-5(n-5)=28-5n
所以:a1=28-5=23、a2=28-5×2=18、a3=28-5×3=13
于是:S3=a1+a2+a3=23+18+13=54
所以: a4+a5+⋯+a10=S10-S3=5-54=-49,选D。