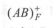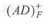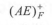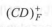参考答案: C D

详细解析:

本题第一空是对候选关键字的考查。

可以利用图示法分析，入度为0的属性集合为｛A,E｝通过该集合出发，可以遍历全图，本题选择C选项。
也可以通过(X)+ F=Y闭包求法分析：
第一步：设最终将成为闭包的属性集是Y，把Y初始化为X；
第二步：检查F中的每一个函数依赖A→B，如果属性集A中所有属性均在Y中，而B中有的属性不在Y中，则将其加入到Y中；
第三步：重复第二步，直到没有属性可以添加到属性集Y中为止。最后得到的Y就是X+
A选项（AB）+ F根据A→BC,C→D可得（AB）+ F ={A,B,C,D} ,
B选项（AD）+ F根据A→BC可得（AD）+ F ={A,B,C,D} ，
C选项（AE）+ F根据A→BC,C→D,AE→G可得（A）+ F={A，B，C，D, E, G}=U ,
D选项（CD）+ F根据C→D可得（CD）+ F ={C，D}。所以第1题答案为C。

本题第二空是对模式分解的考查。

A选项：分解R1(A,B,C) 和R2(D,E,G)，可得F1={A→BC}，F2为空，所以F=F1+F2={ A→BC }，丢失函数依赖C→D,AE→G，所以分解后的关系模式不保持函数依赖。
B选项：分解R1(B,C,D,E) 和R{(A,E,G)，可得F1={C→D}，F2={ AE→G }，所以F=F1+F2={ C→D ，AE→G }，丢失函数依赖A→BC，所以分解后的关系模式不保持函数依赖。
C选项：分解R1(B,C,D) 和R2(A,E,G)，可得F1={C→D}，F2={ AE→G }，所以F=F1+F2={ C→D ，AE→G }，丢失函数依赖A→BC，所以分解后的关系模式不保持函数依赖。
D选项：分解R1(A,B,C,D) 和R2(A,E,G)，可得F1={ A→BC，C→D}，F2={ AE→G }，所以F=F1+F2={ A→BC，C→D ，AE→G }，没有丢失函数依赖，所以分解后的关系模式保持函数依赖。第2题答案为D。