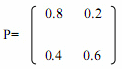参考答案: D

详细解析:

根据题意，该地区冰箱品牌A与B每月占有率的变化描述为常数转移矩阵P。不管初始时刻这两种品牌的市场占有率（以概率向量来描述）如何，最终将稳定到概率向量Z，而且有关系式ZP=Z。这表明，Z的下一时刻仍然是Z。
设Z=(Z₁，Z₂），其中Z₁ ≥0，Z₂ ≥0， Z₁+Z₂=1，从ZP=Z可以列出方程：
0.8Z₁＋0.4Z₂＝Z₁
0.2Z₁＋0.6Z₂＝Z₂
根据上述条件，求解该方程，得到Z₁=2/3，Z₂=1/3。
因此，冰箱品牌A与B在该地区最终将逐步稳定到市场占有率（2/3， 1/3）。品牌A将占有2/3的市场，品牌B将占有1/3的市场。