参考答案: B
详细解析:
答案:B
【考点判断】等差数列求和公式
【解题必知】
①在等差数列{ an}中,若k+l=m+n,则ak+al=am+an
②等差数列求和公式: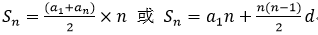
【解题思路】先根据等差数列的单调性结合条件判断出数列正负交界项,再利用下标和定理进行求和转化。
【解题步骤】
由a2003∙a2004<0得,a2003、a2004一正一负,结合a1>0可知,数列单调递减
故a2003>0、a2004<0
结合等差数列下标和定理:
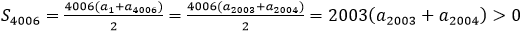
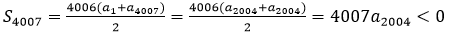
故使Sn>0成立的最大自然数是4006,选B。
若{an}是等差数列,已知a1>0,a2003+a2004>0,a2003∙a2004<0,则使前n项和Sn>0成立的最大自然数是( )
A. 4005
B. 4006
C. 4007
D. 4008
E. 4009
参考答案: B
详细解析:
答案:B
【考点判断】等差数列求和公式
【解题必知】
①在等差数列{ an}中,若k+l=m+n,则ak+al=am+an
②等差数列求和公式: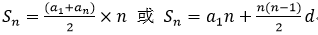
【解题思路】先根据等差数列的单调性结合条件判断出数列正负交界项,再利用下标和定理进行求和转化。
【解题步骤】
由a2003∙a2004<0得,a2003、a2004一正一负,结合a1>0可知,数列单调递减
故a2003>0、a2004<0
结合等差数列下标和定理:
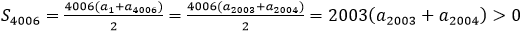
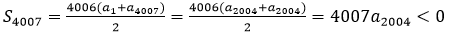
故使Sn>0成立的最大自然数是4006,选B。