参考答案: A
详细解析:
本题考查的是空间几何体的问题,连接AD',因为C'D'⊥DD',C'D'⊥A'D',则C'D'⊥平面AA'D'D,所以C'D'⊥AD',因此∆AD'F是直角三角形,有D'F²+AD'²=AF²。已知D'F=1,AD'为正方形对角线=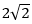 ,所以AF=3.
,所以AF=3.
如图所示,正方体ABCD-A'B'C'D'的棱长为2,F是棱C'D'的中点,则AF的长为( ).
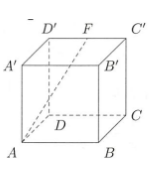
A. 3
B. 5
C. 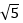
D. 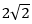
E. 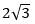
参考答案: A
详细解析:
本题考查的是空间几何体的问题,连接AD',因为C'D'⊥DD',C'D'⊥A'D',则C'D'⊥平面AA'D'D,所以C'D'⊥AD',因此∆AD'F是直角三角形,有D'F²+AD'²=AF²。已知D'F=1,AD'为正方形对角线=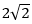 ,所以AF=3.
,所以AF=3.