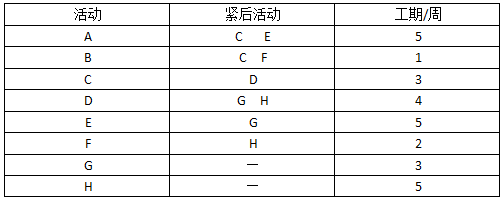
参考答案:
【问题1】
项目的关键路径为ACDH,(1分)项目完成至少需要17周。(1分)增加的限制条件对项目工期没有影响,项目还是需要17周才能完成。(2分)
【问题2】
(1)没有外部条件限制:B的总时差为4,自由时差为0;G的总时差为2,自由时差为2。(2分)
(2)问题1中涉及的外部条件的限制:B的总时差为4,自由时差为0;G的总时差为1,自由时差为1。(3分)
【问题3】
BAC=280万元,项目所有活动共需要5+1+3+4+5+2+3+5=28周,所以单项活动每周的预算为10万元。第一周只有A和B两个活动在同时进行,所以第一周的预算为20万元。(2分)
所有活动的总时间为5+1+3+4+5+2+3+8=28周,项目预算为280万元,平均分布每周10万元。
10周结束时,计划要完成ABCEF活动,且D活动要完成2周任务,则PV=5*10+1*10+3*10+5*10+2*10+2*10=180(1分)
实际完成ABCEF活动,则EV=5*10+1*10+3*10+5*10+2*10=160(1分)
CPI=EV/AC=160/200=0.80(1分)
SPI=EV/PV=160/180=0.89(1分)
详细解析:
该题目是一道综合题,考察考生的项目进度控制和成本控制管理的问题。知识点包括网络图绘制,以及在网络图上计算ES、EF、LS、LF、总时差、自由时差等。利用挣得值法分析和解决问题。【问题1】
先画出网络图,使用正推法计算每个活动的最早开始时间和最早结束时间,最晚开始时间和最晚结束时间。
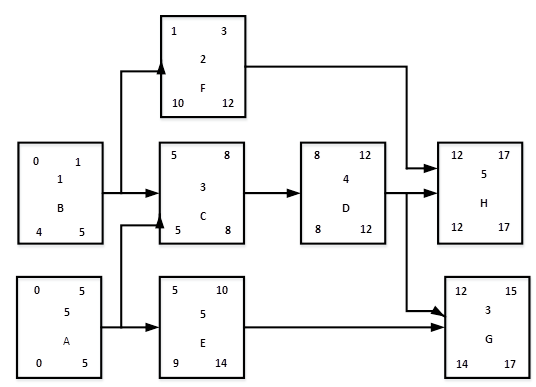
关键路径是总时差为零的活动序列,各个活动的总时差=LS-ES,分别有活动A、C、D、H的总时差为0,所以关键路径是ACDH。
正推法计算得到的最后一个活动最早完成时间的最大值就是项目的最大工期,即H活动的最早完成时间为17就是项目的工期。
因为活动E的总差为4周,大于约束条件3周,活动F的总差为9周,大于约束条件5周,所以项目依旧需要17周。
【问题2】
先分析没有外部条件限制的情况下活动B、活动G的总时差和自由时差:
活动B的总时差等于活动B的最迟完成时间减去最早完成时间,即5-1=4周。
活动B的自由时差等于紧后活动F与活动C的最早开始时间的最小值减去活动B的最早完成时间,即1-1=0周。
活动G的总时差等于活动G的最迟完成时间减去最早完成时间,即17-15-2周。
活动G的自由时差等于紧后活动H的最早开始时间减去活动G的最早完成时间,即17-15=2周。
再分析问题1中涉及外部条件的情况下活动B、活动G、的总时差和自由时差:
问题1的外部约束条件,E活动结束3周后G活动才能开始,可理解为,活动E的工期延长3周,即活动E的工期为8周。F活动开始5周后H活动才可以开始,同样可以理解为活动F的工期延长了5周,即活动F的工期为7周。
在涉及外部条件的情况下,因为F活动的约束条件对关键路径没有影响,所以活动B的总时差等于活动B的最迟开始时间减去最早开始时间,即5-1=4周。
活动B的自由时差等于紧后活动F与活动C的最早开始时间的最小值减去活动B的最早完成时间,即1-1=0周。
活动E的工作期为8周后,G活动最早开始时间为13周,最早完成时间为16周,所以:
活动G的总时差等于活动G的最迟完成时间减去最早完成时间,即17-16=1周。
活动G的自由时差等于活动H的最迟完成时间减去活动G的最早完成时间,即17-16=1周。
【问题3】
BAC=280万元,项目所有活动共需要5+1+3+4+5+2+3+5=28周,则单项活动每周的预算为10万元。项目第一周共有活动A和B进行,所以第一周的预算为20万元。
按照外部条件约束,在第10周应该完成的工作包括A、B、C、E、F、D的2周工作,总计18周工作。
PV=10万元*18周=180万元;
EV=160万元(即实际完成的A、B、C、E、F活动的价值是160万元);
AC=200万元;
可以计算出:
CPI=EV/AC=160/200=0.8
SPI=EV/PV=160/180=0.89
正推法计算得到的最后一个活动最早完成时间的最大值就是项目的最大工期,即H活动的最早完成时间为17就是项目的工期。
因为活动E的总差为4周,大于约束条件3周,活动F的总差为9周,大于约束条件5周,所以项目依旧需要17周。
【问题2】
先分析没有外部条件限制的情况下活动B、活动G的总时差和自由时差:
活动B的总时差等于活动B的最迟完成时间减去最早完成时间,即5-1=4周。
活动B的自由时差等于紧后活动F与活动C的最早开始时间的最小值减去活动B的最早完成时间,即1-1=0周。
活动G的总时差等于活动G的最迟完成时间减去最早完成时间,即17-15-2周。
活动G的自由时差等于紧后活动H的最早开始时间减去活动G的最早完成时间,即17-15=2周。
再分析问题1中涉及外部条件的情况下活动B、活动G、的总时差和自由时差:
问题1的外部约束条件,E活动结束3周后G活动才能开始,可理解为,活动E的工期延长3周,即活动E的工期为8周。F活动开始5周后H活动才可以开始,同样可以理解为活动F的工期延长了5周,即活动F的工期为7周。
在涉及外部条件的情况下,因为F活动的约束条件对关键路径没有影响,所以活动B的总时差等于活动B的最迟开始时间减去最早开始时间,即5-1=4周。
活动B的自由时差等于紧后活动F与活动C的最早开始时间的最小值减去活动B的最早完成时间,即1-1=0周。
活动E的工作期为8周后,G活动最早开始时间为13周,最早完成时间为16周,所以:
活动G的总时差等于活动G的最迟完成时间减去最早完成时间,即17-16=1周。
活动G的自由时差等于活动H的最迟完成时间减去活动G的最早完成时间,即17-16=1周。
【问题3】
BAC=280万元,项目所有活动共需要5+1+3+4+5+2+3+5=28周,则单项活动每周的预算为10万元。项目第一周共有活动A和B进行,所以第一周的预算为20万元。
按照外部条件约束,在第10周应该完成的工作包括A、B、C、E、F、D的2周工作,总计18周工作。
PV=10万元*18周=180万元;
EV=160万元(即实际完成的A、B、C、E、F活动的价值是160万元);
AC=200万元;
可以计算出:
CPI=EV/AC=160/200=0.8
SPI=EV/PV=160/180=0.89