参考答案: D
详细解析:
【考点判断】乘法公式的应用
【解题必知】
①配方公式: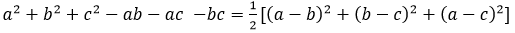
②对于连比式(多个等号连接起来的分数表达式),可采用设“k”法:令整个式子为k,然后
分别在每部分式子中得出字母与k的关系。
【解题思路】再每个条件下凑出x+y+z的表达式,根据对应公示判断其正负。
一、判断条件(1),代入题干,即判断“已知a、b、c是不全相等的任意实数,x= a²-bc、y= b²-ac、z=c²-ab.,则实数x、y、z中至少有一个为正数”是否成立。
已知a、b、c是不全相等的任意实数,
由三项配方公式得: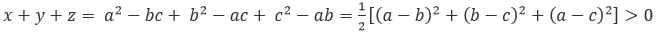
x、y、z之和为正,则x、y、z中至少有一个为正数,条件充分。
二、判断条件(2),代入题干,即判断“已知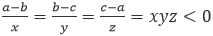 ,则实数x、y、z中至少有一个为正数”是否成立。
,则实数x、y、z中至少有一个为正数”是否成立。
由 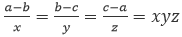 ,
,
可得
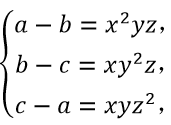
三个式子相加,可得x²yz+ xy²z+ xyz²=0,即xyz(x+y+z)=0
又xyz<0,故x+y+z=0,且、y、z三个数均不为0。
所以,x、y、z中至少有一个数为正数,条件(2)充分。
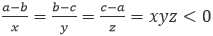 .
.