参考答案: C

详细解析:

答案：C
【考点判断】最值问题
【解题必知】
①最值问题题干出现明显的变量关系，则要想到构造函数，通过求函数的最值解决
②二次函数y=ax²+bx+c，对称轴为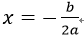：，顶点坐标为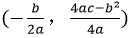

③无范围限制的二次函数的最值一定在顶点取得，顶点一定在对称轴上。对于在x有范围限制的二次函数求最值，最值必在端点或顶点位置取得，若顶点不在范围内，则只能在两端点出取最值。
【解题思路】设变量上涨的租金为x个50元，根据利润=销售收入-总成本列出函数表达式，求函数的最值即可。
【解题步骤】

设每辆车每月的租金上涨x个50元，所以少租出x辆车。
于是每月每辆车的收入为(3000+50x-150)，租出去的车有(100-x)辆
另有未租出去车辆额外维护费成本50x
则月收入为f(x)=(3000+50x-150)(100-x)-50x，
整理得 f(x)=-50x²+2100x+285000=-50(x-21)²+307050  ，
解得x=21时，f(x)取得最大值，所以每月租金应为3000+50x=4050元。