C++14(g++5.4) 解法, 执行用时: 125ms, 内存消耗: 9140K, 提交时间: 2019-11-07 13:25:10
#include <bits/stdc++.h>
#define ll long long
#define sc scanf
#define pr printf
using namespace std;
const int MAXN = 1e5 + 5;
struct edge
{
int to;
ll dis;
int nex;
}e[MAXN * 2];
int head[MAXN], tot;
void init()
{
memset(head, -1, sizeof(head));
tot = 0;
}
void add(int in, int to, ll dis)
{
e[tot] = edge{ to,dis,head[in] };
head[in] = tot++;
}
bool vis[MAXN];
ll val[MAXN];
struct LB
{
static const int wei = 63;
ll b[wei + 1], cnt;//cnt是个数
void init()
{
cnt = 0;
memset(b, 0, sizeof(b));
}
bool insert(ll x)//插入
{
for (int i = wei; i >= 0; i--)
{
if (x & (1LL << i))
{
if (!b[i])
{
b[i] = x;
cnt++;
return true;
}
x ^= b[i];
}
}
return false;
}
ll Max(ll x)//与x异或的最大值
{
ll res = x;
for (int i = wei; i >= 0; i--)
res = max(res, res ^ b[i]);
return res;
}
}lb;
int n, m;
void dfs(int u)
{
vis[u] = true;
for (int i = head[u]; i + 1; i = e[i].nex)
{
int to = e[i].to;
if (vis[to])
lb.insert(val[u] ^ e[i].dis ^ val[to]);
else
{
val[to] = val[u] ^ e[i].dis;
dfs(to);
}
}
}
int main()
{
init();
sc("%d%d", &n, &m);
while (m--)
{
int a, b; ll c;
sc("%d%d%lld", &a, &b, &c);
add(a, b, c);
add(b, a, c);
}
dfs(1);
ll ans = lb.Max(val[n]);
pr("%lld\n", ans);
}
C++11(clang++ 3.9) 解法, 执行用时: 239ms, 内存消耗: 30840K, 提交时间: 2020-03-03 10:28:42
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int INF=0x3f3f3f3f;
const int MOD=10000007;
const int maxn=1e6+10;
int n,m;
struct edge
{
int to;
LL w;
};
vector<edge> g[maxn];
LL d[maxn];
void insert(LL x)
{
for(int i=60;i>=0;i--)
{
if((x>>i)&1)
{
if(!d[i])
{
d[i]=x;
break;
}
else
x^=d[i];
}
}
}
LL query_max(LL x)
{
LL ans=x;
for(int i=60;i>=0;i--)
ans=max(ans,ans^d[i]);
return ans;
}
bool vis[maxn];
LL dist[maxn];
void DFS(int u)
{
vis[u]=true;
for(auto it:g[u])
{
int v=it.to;
LL w=it.w;
if(!vis[v])
{
dist[v]=dist[u]^w;
DFS(v);
}
else
insert(dist[u]^dist[v]^w);
}
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=1;i<=m;i++)
{
int u,v;
LL w;
scanf("%d %d %lld",&u,&v,&w);
g[u].push_back(edge{v,w});
g[v].push_back(edge{u,w});
}
DFS(1);
printf("%lld\n",query_max(dist[n]));
return 0;
}
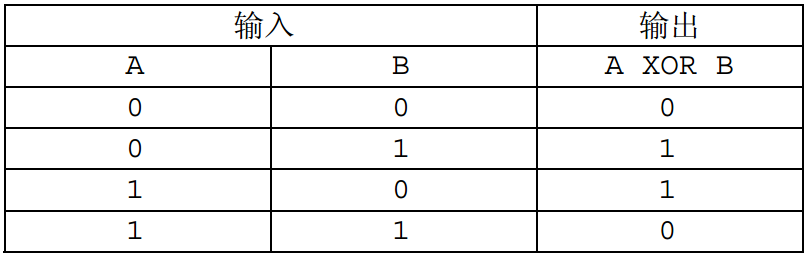
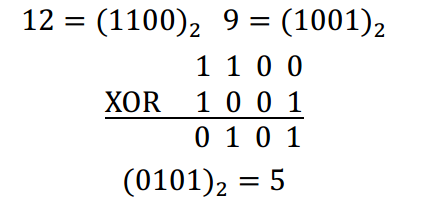
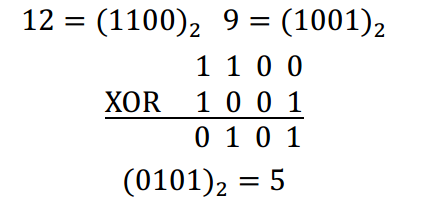
A的 XOR 和为
,
,
,表示
与
之间存在一条权值为
的无向边。
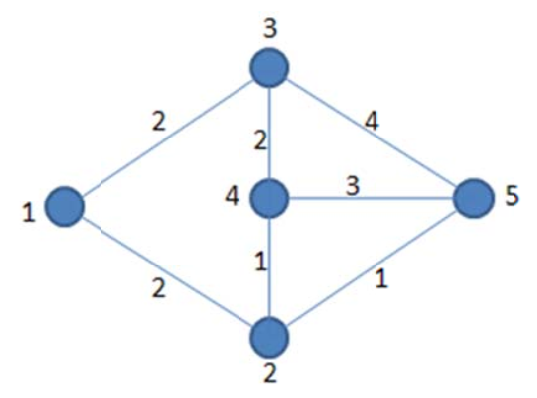
对应的XOR和为
对应的XOR和也是2 XOR 4 = 6。