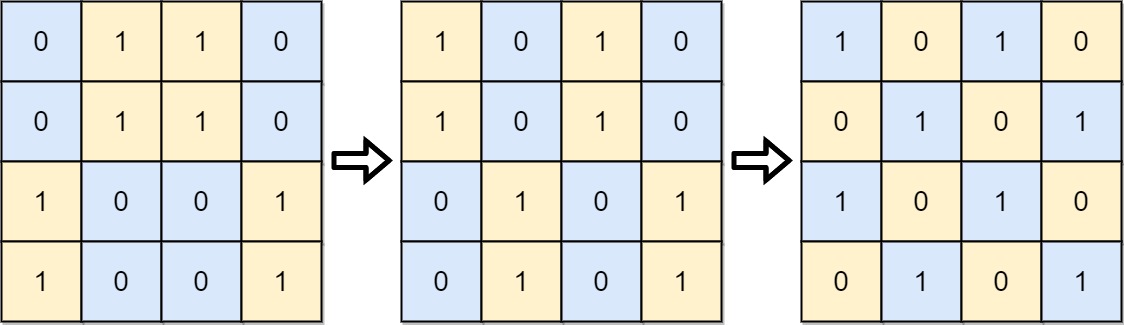
上次编辑到这里,代码来自缓存 点击恢复默认模板
class Solution {
public:
int movesToChessboard(vector<vector<int>>& board) {
}
};
cpp 解法, 执行用时: 8 ms, 内存消耗: 10.2 MB, 提交时间: 2023-09-28 15:34:52
class Solution {
public:
int getMoves(int mask, int count, int n) {
int ones = __builtin_popcount(mask);
if (n & 1) {
/* 如果 n 为奇数,则每一行中 1 与 0 的数目相差为 1,且满足相邻行交替 */
if (abs(n - 2 * ones) != 1 || abs(n - 2 * count) != 1 ) {
return -1;
}
if (ones == (n >> 1)) {
/* 偶数位变为 1 的最小交换次数 */
return n / 2 - __builtin_popcount(mask & 0xAAAAAAAA);
} else {
/* 奇数位变为 1 的最小交换次数 */
return (n + 1) / 2 - __builtin_popcount(mask & 0x55555555);
}
} else {
/* 如果 n 为偶数,则每一行中 1 与 0 的数目相等,且满足相邻行交替 */
if (ones != (n >> 1) || count != (n >> 1)) {
return -1;
}
/* 偶数位变为 1 的最小交换次数 */
int count0 = n / 2 - __builtin_popcount(mask & 0xAAAAAAAA);
/* 奇数位变为 1 的最小交换次数 */
int count1 = n / 2 - __builtin_popcount(mask & 0x55555555);
return min(count0, count1);
}
}
int movesToChessboard(vector<vector<int>>& board) {
int n = board.size();
int rowMask = 0, colMask = 0;
/* 检查棋盘的第一行与第一列 */
for (int i = 0; i < n; i++) {
rowMask |= (board[0][i] << i);
colMask |= (board[i][0] << i);
}
int reverseRowMask = ((1 << n) - 1) ^ rowMask;
int reverseColMask = ((1 << n) - 1) ^ colMask;
int rowCnt = 0, colCnt = 0;
for (int i = 0; i < n; i++) {
int currRowMask = 0;
int currColMask = 0;
for (int j = 0; j < n; j++) {
currRowMask |= (board[i][j] << j);
currColMask |= (board[j][i] << j);
}
/* 检测每一行的状态是否合法 */
if (currRowMask != rowMask && currRowMask != reverseRowMask) {
return -1;
} else if (currRowMask == rowMask) {
/* 记录与第一行相同的行数 */
rowCnt++;
}
/* 检测每一列的状态是否合法 */
if (currColMask != colMask && currColMask != reverseColMask) {
return -1;
} else if (currColMask == colMask) {
/* 记录与第一列相同的列数 */
colCnt++;
}
}
int rowMoves = getMoves(rowMask, rowCnt, n);
int colMoves = getMoves(colMask, colCnt, n);
return (rowMoves == -1 || colMoves == -1) ? -1 : (rowMoves + colMoves);
}
};
java 解法, 执行用时: 1 ms, 内存消耗: 41.9 MB, 提交时间: 2023-09-28 15:34:39
class Solution {
public int movesToChessboard(int[][] board) {
int n = board.length;
int rowMask = 0, colMask = 0;
/* 检查棋盘的第一行与第一列 */
for (int i = 0; i < n; i++) {
rowMask |= (board[0][i] << i);
colMask |= (board[i][0] << i);
}
int reverseRowMask = ((1 << n) - 1) ^ rowMask;
int reverseColMask = ((1 << n) - 1) ^ colMask;
int rowCnt = 0, colCnt = 0;
for (int i = 0; i < n; i++) {
int currRowMask = 0;
int currColMask = 0;
for (int j = 0; j < n; j++) {
currRowMask |= (board[i][j] << j);
currColMask |= (board[j][i] << j);
}
/* 检测每一行的状态是否合法 */
if (currRowMask != rowMask && currRowMask != reverseRowMask) {
return -1;
} else if (currRowMask == rowMask) {
/* 记录与第一行相同的行数 */
rowCnt++;
}
/* 检测每一列的状态是否合法 */
if (currColMask != colMask && currColMask != reverseColMask) {
return -1;
} else if (currColMask == colMask) {
/* 记录与第一列相同的列数 */
colCnt++;
}
}
int rowMoves = getMoves(rowMask, rowCnt, n);
int colMoves = getMoves(colMask, colCnt, n);
return (rowMoves == -1 || colMoves == -1) ? -1 : (rowMoves + colMoves);
}
public int getMoves(int mask, int count, int n) {
int ones = Integer.bitCount(mask);
if ((n & 1) == 1) {
/* 如果 n 为奇数,则每一行中 1 与 0 的数目相差为 1,且满足相邻行交替 */
if (Math.abs(n - 2 * ones) != 1 || Math.abs(n - 2 * count) != 1 ) {
return -1;
}
if (ones == (n >> 1)) {
/* 以 0 为开头的最小交换次数 */
return n / 2 - Integer.bitCount(mask & 0xAAAAAAAA);
} else {
return (n + 1) / 2 - Integer.bitCount(mask & 0x55555555);
}
} else {
/* 如果 n 为偶数,则每一行中 1 与 0 的数目相等,且满足相邻行交替 */
if (ones != (n >> 1) || count != (n >> 1)) {
return -1;
}
/* 找到行的最小交换次数 */
int count0 = n / 2 - Integer.bitCount(mask & 0xAAAAAAAA);
int count1 = n / 2 - Integer.bitCount(mask & 0x55555555);
return Math.min(count0, count1);
}
}
}
python3 解法, 执行用时: 44 ms, 内存消耗: 16 MB, 提交时间: 2023-09-28 15:34:25
class Solution:
def movesToChessboard(self, board: List[List[int]]) -> int:
n = len(board)
# 棋盘的第一行与第一列
rowMask = colMask = 0
for i in range(n):
rowMask |= board[0][i] << i
colMask |= board[i][0] << i
reverseRowMask = ((1 << n) - 1) ^ rowMask
reverseColMask = ((1 << n) - 1) ^ colMask
rowCnt = colCnt = 0
for i in range(n):
currRowMask = currColMask = 0
for j in range(n):
currRowMask |= board[i][j] << j
currColMask |= board[j][i] << j
# 检测每一行和每一列的状态是否合法
if currRowMask != rowMask and currRowMask != reverseRowMask or \
currColMask != colMask and currColMask != reverseColMask:
return -1
rowCnt += currRowMask == rowMask # 记录与第一行相同的行数
colCnt += currColMask == colMask # 记录与第一列相同的列数
def getMoves(mask: int, count: int) -> int:
ones = mask.bit_count()
if n & 1:
# 如果 n 为奇数,则每一行中 1 与 0 的数目相差为 1,且满足相邻行交替
if abs(n - 2 * ones) != 1 or abs(n - 2 * count) != 1:
return -1
if ones == n // 2:
# 偶数位变为 1 的最小交换次数
return n // 2 - (mask & 0xAAAAAAAA).bit_count()
else:
# 奇数位变为 1 的最小交换次数
return (n + 1) // 2 - (mask & 0x55555555).bit_count()
else:
# 如果 n 为偶数,则每一行中 1 与 0 的数目相等,且满足相邻行交替
if ones != n // 2 or count != n // 2:
return -1
# 偶数位变为 1 的最小交换次数
count0 = n // 2 - (mask & 0xAAAAAAAA).bit_count()
# 奇数位变为 1 的最小交换次数
count1 = n // 2 - (mask & 0x55555555).bit_count()
return min(count0, count1)
rowMoves = getMoves(rowMask, rowCnt)
colMoves = getMoves(colMask, colCnt)
return -1 if rowMoves == -1 or colMoves == -1 else rowMoves + colMoves
javascript 解法, 执行用时: 64 ms, 内存消耗: 42.9 MB, 提交时间: 2023-09-28 15:34:11
/**
* @param {number[][]} board
* @return {number}
*/
var movesToChessboard = function(board) {
const n = board.length;
let rowMask = 0, colMask = 0;
/* 检查棋盘的第一行与第一列 */
for (let i = 0; i < n; i++) {
rowMask |= (board[0][i] << i);
colMask |= (board[i][0] << i);
}
const reverseRowMask = ((1 << n) - 1) ^ rowMask;
const reverseColMask = ((1 << n) - 1) ^ colMask;
let rowCnt = 0, colCnt = 0;
for (let i = 0; i < n; i++) {
let currRowMask = 0;
let currColMask = 0;
for (let j = 0; j < n; j++) {
currRowMask |= (board[i][j] << j);
currColMask |= (board[j][i] << j);
}
/* 检测每一行的状态是否合法 */
if (currRowMask !== rowMask && currRowMask !== reverseRowMask) {
return -1;
} else if (currRowMask === rowMask) {
/* 记录与第一行相同的行数 */
rowCnt++;
}
/* 检测每一列的状态是否合法 */
if (currColMask !== colMask && currColMask !== reverseColMask) {
return -1;
} else if (currColMask === colMask) {
/* 记录与第一列相同的列数 */
colCnt++;
}
}
const rowMoves = getMoves(rowMask, rowCnt, n);
const colMoves = getMoves(colMask, colCnt, n);
return (rowMoves == -1 || colMoves == -1) ? -1 : (rowMoves + colMoves);
};
const getMoves = (mask, count, n) => {
const ones = bitCount(mask);
if ((n & 1) === 1) {
/* 如果 n 为奇数,则每一行中 1 与 0 的数目相差为 1,且满足相邻行交替 */
if (Math.abs(n - 2 * ones) !== 1 || Math.abs(n - 2 * count) !== 1 ) {
return -1;
}
if (ones === (n >> 1)) {
/* 以 0 为开头的最小交换次数 */
return Math.floor(n / 2) - bitCount(mask & 0xAAAAAAAA);
} else {
return Math.floor((n + 1) / 2) - bitCount(mask & 0x55555555);
}
} else {
/* 如果 n 为偶数,则每一行中 1 与 0 的数目相等,且满足相邻行交替 */
if (ones !== (n >> 1) || count !== (n >> 1)) {
return -1;
}
/* 找到行的最小交换次数 */
const count0 = Math.floor(n / 2) - bitCount(mask & 0xAAAAAAAA);
const count1 = Math.floor(n / 2) - bitCount(mask & 0x55555555);
return Math.min(count0, count1);
}
}
const bitCount = (num) => {
return num.toString(2).split('0').join('').length
}
golang 解法, 执行用时: 8 ms, 内存消耗: 3.6 MB, 提交时间: 2023-09-28 15:33:55
func getMoves(mask uint, count, n int) int {
ones := bits.OnesCount(mask)
if n&1 > 0 {
// 如果 n 为奇数,则每一行中 1 与 0 的数目相差为 1,且满足相邻行交替
if abs(n-2*ones) != 1 || abs(n-2*count) != 1 {
return -1
}
if ones == n>>1 {
// 偶数位变为 1 的最小交换次数
return n/2 - bits.OnesCount(mask&0xAAAAAAAA)
} else {
// 奇数位变为 1 的最小交换次数
return (n+1)/2 - bits.OnesCount(mask&0x55555555)
}
} else {
// 如果 n 为偶数,则每一行中 1 与 0 的数目相等,且满足相邻行交替
if ones != n>>1 || count != n>>1 {
return -1
}
// 偶数位变为 1 的最小交换次数
count0 := n/2 - bits.OnesCount(mask&0xAAAAAAAA)
// 奇数位变为 1 的最小交换次数
count1 := n/2 - bits.OnesCount(mask&0x55555555)
return min(count0, count1)
}
}
func movesToChessboard(board [][]int) int {
n := len(board)
// 棋盘的第一行与第一列
rowMask, colMask := 0, 0
for i := 0; i < n; i++ {
rowMask |= board[0][i] << i
colMask |= board[i][0] << i
}
reverseRowMask := 1<<n - 1 ^ rowMask
reverseColMask := 1<<n - 1 ^ colMask
rowCnt, colCnt := 0, 0
for i := 0; i < n; i++ {
currRowMask, currColMask := 0, 0
for j := 0; j < n; j++ {
currRowMask |= board[i][j] << j
currColMask |= board[j][i] << j
}
if currRowMask != rowMask && currRowMask != reverseRowMask || // 检测每一行的状态是否合法
currColMask != colMask && currColMask != reverseColMask { // 检测每一列的状态是否合法
return -1
}
if currRowMask == rowMask {
rowCnt++ // 记录与第一行相同的行数
}
if currColMask == colMask {
colCnt++ // 记录与第一列相同的列数
}
}
rowMoves := getMoves(uint(rowMask), rowCnt, n)
colMoves := getMoves(uint(colMask), colCnt, n)
if rowMoves == -1 || colMoves == -1 {
return -1
}
return rowMoves + colMoves
}
func abs(x int) int {
if x < 0 {
return -x
}
return x
}
func min(a, b int) int {
if a > b {
return b
}
return a
}