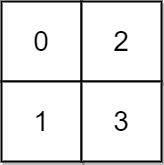
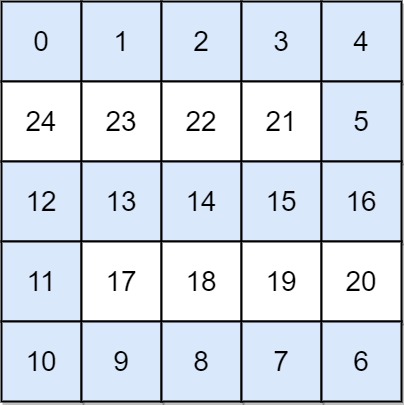
C++
Java
Python
Python3
C
C#
JavaScript
Ruby
Swift
Go
Scala
Kotlin
Rust
PHP
TypeScript
Racket
Erlang
Elixir
Dart
monokai
ambiance
chaos
chrome
cloud9_day
cloud9_night
cloud9_night_low_color
clouds
clouds_midnight
cobalt
crimson_editor
dawn
dracula
dreamweaver
eclipse
github
github_dark
gob
gruvbox
gruvbox_dark_hard
gruvbox_light_hard
idle_fingers
iplastic
katzenmilch
kr_theme
kuroir
merbivore
merbivore_soft
mono_industrial
nord_dark
one_dark
pastel_on_dark
solarized_dark
solarized_light
sqlserver
terminal
textmate
tomorrow
tomorrow_night
tomorrow_night_blue
tomorrow_night_bright
tomorrow_night_eighties
twilight
vibrant_ink
xcode
上次编辑到这里,代码来自缓存 点击恢复默认模板
class Solution {
public:
int swimInWater(vector<vector<int>>& grid) {
}
};
运行代码
提交
java 解法, 执行用时: 14 ms, 内存消耗: 42.1 MB, 提交时间: 2023-09-26 19:57:58
import java.util.Arrays;
import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.Queue;
public class Solution {
// Dijkstra 算法(应用前提:没有负权边,找单源最短路径)
public int swimInWater(int[][] grid) {
int n = grid.length;
Queue<int[]> minHeap = new PriorityQueue<>(Comparator.comparingInt(o -> grid[o[0]][o[1]]));
minHeap.offer(new int[]{0, 0});
boolean[][] visited = new boolean[n][n];
// distTo[i][j] 表示:到顶点 [i, j] 须要等待的最少的时间
int[][] distTo = new int[n][n];
for (int[] row : distTo) {
Arrays.fill(row, n * n);
}
distTo[0][0] = grid[0][0];
int[][] directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
while (!minHeap.isEmpty()) {
// 找最短的边
int[] front = minHeap.poll();
int currentX = front[0];
int currentY = front[1];
if (visited[currentX][currentY]) {
continue;
}
// 确定最短路径顶点
visited[currentX][currentY] = true;
if (currentX == n - 1 && currentY == n - 1) {
return distTo[n - 1][n - 1];
}
// 更新
for (int[] direction : directions) {
int newX = currentX + direction[0];
int newY = currentY + direction[1];
if (inArea(newX, newY, n) && !visited[newX][newY] &&
Math.max(distTo[currentX][currentY], grid[newX][newY]) < distTo[newX][newY]) {
distTo[newX][newY] = Math.max(distTo[currentX][currentY], grid[newX][newY]);
minHeap.offer(new int[]{newX, newY});
}
}
}
return -1;
}
private boolean inArea(int x, int y, int n) {
return x >= 0 && x < n && y >= 0 && y < n;
}
}
java 解法, 执行用时: 6 ms, 内存消耗: 41.5 MB, 提交时间: 2023-09-26 19:57:42
public class Solution {
private int N;
public static final int[][] DIRECTIONS = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
public int swimInWater(int[][] grid) {
this.N = grid.length;
int len = N * N;
// 下标:方格的高度,值:对应在方格中的坐标
int[] index = new int[len];
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
index[grid[i][j]] = getIndex(i, j);
}
}
UnionFind unionFind = new UnionFind(len);
for (int i = 0; i < len; i++) {
int x = index[i] / N;
int y = index[i] % N;
for (int[] direction : DIRECTIONS) {
int newX = x + direction[0];
int newY = y + direction[1];
if (inArea(newX, newY) && grid[newX][newY] <= i) {
unionFind.union(index[i], getIndex(newX, newY));
}
if (unionFind.isConnected(0, len - 1)) {
return i;
}
}
}
return -1;
}
private int getIndex(int x, int y) {
return x * N + y;
}
private boolean inArea(int x, int y) {
return x >= 0 && x < N && y >= 0 && y < N;
}
private class UnionFind {
private int[] parent;
public UnionFind(int n) {
this.parent = new int[n];
for (int i = 0; i < n; i++) {
parent[i] = i;
}
}
public int root(int x) {
while (x != parent[x]) {
parent[x] = parent[parent[x]];
x = parent[x];
}
return x;
}
public boolean isConnected(int x, int y) {
return root(x) == root(y);
}
public void union(int p, int q) {
if (isConnected(p, q)) {
return;
}
parent[root(p)] = root(q);
}
}
}
java 解法, 执行用时: 8 ms, 内存消耗: 42.6 MB, 提交时间: 2023-09-26 19:57:24
import java.util.LinkedList;
import java.util.Queue;
public class Solution {
private int N;
public static final int[][] DIRECTIONS = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
public int swimInWater(int[][] grid) {
this.N = grid.length;
int left = 0;
int right = N * N - 1;
while (left < right) {
int mid = (left + right) / 2;
if (grid[0][0] <= mid && bfs(grid, mid)) {
// mid 可以,尝试 mid 小一点是不是也可以呢?// [left, mid]
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
/**
* 使用广度优先遍历得到从 (x, y) 开始向四个方向的所有小于等于 threshold 且与 (x, y) 连通的结点
*
* @param grid
* @param threshold
* @return
*/
private boolean bfs(int[][] grid, int threshold) {
Queue<int[]> queue = new LinkedList<>();
queue.offer(new int[]{0, 0});
boolean[][] visited = new boolean[N][N];
visited[0][0] = true;
while (!queue.isEmpty()) {
int[] front = queue.poll();
int x = front[0];
int y = front[1];
for (int[] direction : DIRECTIONS) {
int newX = x + direction[0];
int newY = y + direction[1];
if (inArea(newX, newY) && !visited[newX][newY] && grid[newX][newY] <= threshold) {
if (newX == N - 1 && newY == N - 1) {
return true;
}
queue.offer(new int[]{newX, newY});
visited[newX][newY] = true;
}
}
}
return false;
}
private boolean inArea(int x, int y) {
return x >= 0 && x < N && y >= 0 && y < N;
}
}
java 解法, 执行用时: 2 ms, 内存消耗: 41.4 MB, 提交时间: 2023-09-26 19:57:13
public class Solution {
private int N;
public static final int[][] DIRECTIONS = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
public int swimInWater(int[][] grid) {
this.N = grid.length;
int left = 0;
int right = N * N - 1;
while (left < right) {
// left + right 不会溢出
int mid = (left + right) / 2;
boolean[][] visited = new boolean[N][N];
if (grid[0][0] <= mid && dfs(grid, 0, 0, visited, mid)) {
// mid 可以,尝试 mid 小一点是不是也可以呢?下一轮搜索的区间 [left, mid]
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
/**
* 使用深度优先遍历得到从 (x, y) 开始向四个方向的所有小于等于 threshold 且与 (x, y) 连通的结点
*
* @param grid
* @param x
* @param y
* @param visited
* @param threshold
* @return
*/
private boolean dfs(int[][] grid, int x, int y, boolean[][] visited, int threshold) {
visited[x][y] = true;
for (int[] direction : DIRECTIONS) {
int newX = x + direction[0];
int newY = y + direction[1];
if (inArea(newX, newY) && !visited[newX][newY] && grid[newX][newY] <= threshold) {
if (newX == N - 1 && newY == N - 1) {
return true;
}
if (dfs(grid, newX, newY, visited, threshold)) {
return true;
}
}
}
return false;
}
private boolean inArea(int x, int y) {
return x >= 0 && x < N && y >= 0 && y < N;
}
}
javascript 解法, 执行用时: 240 ms, 内存消耗: 50.7 MB, 提交时间: 2023-09-26 19:56:11
/**
* @param {number[][]} grid
* @return {number}
*/
var swimInWater = function(grid) {
let ARR = [[0,1],[0,-1],[1,0],[-1,0]];
//记录所有已经访问过的点
let dp = new Array(grid.length).fill(0).map(i=>new Array(grid[0].length).fill(0));
let result = 0;
let stack=[[0,0]];
while(stack.length>0){
let [row,col] = stack.shift();
//用以记录当前已经保存的所有能走的点
result = Math.max(result,grid[row][col]);
if(row===grid.length-1 && col===grid[0].length-1){
//达到终点结束遍历
break;
}
for(let [dr,dc] of ARR){
let [nr,nc] = [dr+row,dc+col];
if(nr<grid.length && nr>=0 && nc<grid[0].length && nc>=0 && !dp[nr][nc]){
dp[nr][nc]=1
//此处若使用二分查找插入还能对时间进行优化
stack.push([nr,nc,grid[nr][nc]])
}
}
//排序还能使用二分插入法进行优化
stack.sort((a,b)=>a[2]-b[2])
}
return result;
};
javascript 解法, 执行用时: 96 ms, 内存消耗: 49 MB, 提交时间: 2023-09-26 19:55:47
/**
* @param {number[][]} grid
* @return {number}
*/
var swimInWater = function(grid) {
const n = grid.length;
let left = 0, right = n * n - 1;
while (left < right) {
const mid = Math.floor((left + right) / 2);
if (check(grid, mid)) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
const check = (grid, threshold) => {
if (grid[0][0] > threshold) {
return false;
}
const n = grid.length;
const visited = new Array(n).fill(0).map(() => new Array(n).fill(false));
visited[0][0] = true;
const queue = [[0, 0]];
const directions = [[0, 1], [0, -1], [1, 0], [-1, 0]];
while (queue.length) {
const square = queue.shift();
const i = square[0], j = square[1];
for (const direction of directions) {
const ni = i + direction[0], nj = j + direction[1];
if (ni >= 0 && ni < n && nj >= 0 && nj < n) {
if (!visited[ni][nj] && grid[ni][nj] <= threshold) {
queue.push([ni, nj]);
visited[ni][nj] = true;
}
}
}
}
return visited[n - 1][n - 1];
}
golang 解法, 执行用时: 12 ms, 内存消耗: 5 MB, 提交时间: 2023-09-26 19:55:16
type entry struct{ i, j, val int }
type hp []entry
func (h hp) Len() int { return len(h) }
func (h hp) Less(i, j int) bool { return h[i].val < h[j].val }
func (h hp) Swap(i, j int) { h[i], h[j] = h[j], h[i] }
func (h *hp) Push(v interface{}) { *h = append(*h, v.(entry)) }
func (h *hp) Pop() interface{} { a := *h; v := a[len(a)-1]; *h = a[:len(a)-1]; return v }
type pair struct{ x, y int }
var dirs = []pair{{-1, 0}, {1, 0}, {0, -1}, {0, 1}}
// 基于最小堆
func swimInWater(grid [][]int) (ans int) {
n := len(grid)
vis := make([][]bool, n)
for i := range vis {
vis[i] = make([]bool, n)
}
vis[0][0] = true
h := &hp{{0, 0, grid[0][0]}}
for {
e := heap.Pop(h).(entry)
ans = max(ans, e.val)
if e.i == n-1 && e.j == n-1 {
return
}
for _, d := range dirs {
if x, y := e.i+d.x, e.j+d.y; 0 <= x && x < n && 0 <= y && y < n && !vis[x][y] {
vis[x][y] = true
heap.Push(h, entry{x, y, grid[x][y]})
}
}
}
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
// 二分查找
func swimInWater2(grid [][]int) (ans int) {
n := len(grid)
return sort.Search(n*n-1, func(threshold int) bool {
if threshold < grid[0][0] {
return false
}
vis := make([][]bool, n)
for i := range vis {
vis[i] = make([]bool, n)
}
vis[0][0] = true
queue := []pair{{}}
for len(queue) > 0 {
p := queue[0]
queue = queue[1:]
for _, d := range dirs {
if x, y := p.x+d.x, p.y+d.y; 0 <= x && x < n && 0 <= y && y < n && !vis[x][y] && grid[x][y] <= threshold {
vis[x][y] = true
queue = append(queue, pair{x, y})
}
}
}
return vis[n-1][n-1]
})
}
java 解法, 执行用时: 7 ms, 内存消耗: 42.4 MB, 提交时间: 2023-09-26 19:53:52
class Solution {
// 二分查找
public int swimInWater(int[][] grid) {
int n = grid.length;
int left = 0, right = n * n - 1;
while (left < right) {
int mid = (left + right) / 2;
if (check(grid, mid)) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
public boolean check(int[][] grid, int threshold) {
if (grid[0][0] > threshold) {
return false;
}
int n = grid.length;
boolean[][] visited = new boolean[n][n];
visited[0][0] = true;
Queue<int[]> queue = new LinkedList<int[]>();
queue.offer(new int[]{0, 0});
int[][] directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
while (!queue.isEmpty()) {
int[] square = queue.poll();
int i = square[0], j = square[1];
for (int[] direction : directions) {
int ni = i + direction[0], nj = j + direction[1];
if (ni >= 0 && ni < n && nj >= 0 && nj < n) {
if (!visited[ni][nj] && grid[ni][nj] <= threshold) {
queue.offer(new int[]{ni, nj});
visited[ni][nj] = true;
}
}
}
}
return visited[n - 1][n - 1];
}
// 堆
public int swimInWater2(int[][] grid) {
int n = grid.length;
PriorityQueue<Entry> pq = new PriorityQueue<Entry>(new Comparator<Entry>() {
public int compare(Entry entry1, Entry entry2) {
return entry1.val - entry2.val;
}
});
boolean[][] visited = new boolean[n][n];
pq.offer(new Entry(0, 0, grid[0][0]));
int ret = 0;
int[][] directions = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
while (!pq.isEmpty()) {
Entry x = pq.poll();
if (visited[x.i][x.j]) {
continue;
}
visited[x.i][x.j] = true;
ret = Math.max(ret, grid[x.i][x.j]);
if (x.i == n - 1 && x.j == n - 1) {
break;
}
for (int[] direction : directions) {
int ni = x.i + direction[0], nj = x.j + direction[1];
if (ni >= 0 && ni < n && nj >= 0 && nj < n) {
if (!visited[ni][nj]) {
pq.offer(new Entry(ni, nj, grid[ni][nj]));
}
}
}
}
return ret;
}
}
// 优先队列中的数据结构。其中 (i,j) 代表坐标,val 代表水位。
class Entry {
int i;
int j;
int val;
public Entry(int i, int j, int val) {
this.i = i;
this.j = j;
this.val = val;
}
};
cpp 解法, 执行用时: 32 ms, 内存消耗: 9.6 MB, 提交时间: 2023-09-26 19:53:02
// 优先队列中的数据结构。其中 (i,j) 代表坐标,val 代表水位。
struct Entry {
int i;
int j;
int val;
bool operator<(const Entry& other) const {
return this->val > other.val;
}
Entry(int ii, int jj, int val): i(ii), j(jj), val(val) {}
};
class Solution {
public:
int swimInWater(vector<vector<int>>& grid) {
int n = grid.size();
priority_queue<Entry, vector<Entry>, function<bool(const Entry& x, const Entry& other)>> pq(&Entry::operator<);
vector<vector<int>> visited(n, vector<int>(n, 0));
pq.push(Entry(0, 0, grid[0][0]));
int ret = 0;
vector<pair<int, int>> directions{{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
while (!pq.empty()) {
Entry x = pq.top();
pq.pop();
if (visited[x.i][x.j] == 1) {
continue;
}
visited[x.i][x.j] = 1;
ret = max(ret, grid[x.i][x.j]);
if (x.i == n - 1 && x.j == n - 1) {
break;
}
for (const auto [di, dj]: directions) {
int ni = x.i + di, nj = x.j + dj;
if (ni >= 0 && ni < n && nj >= 0 && nj < n) {
if (visited[ni][nj] == 0) {
pq.push(Entry(ni, nj, grid[ni][nj]));
}
}
}
}
return ret;
}
// 二分查找
bool check(vector<vector<int>>& grid, int threshold) {
if (grid[0][0] > threshold) {
return false;
}
int n = grid.size();
vector<vector<int>> visited(n, vector<int>(n, 0));
visited[0][0] = 1;
queue<pair<int, int>> q;
q.push(make_pair(0, 0));
vector<pair<int, int>> directions{{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
while (!q.empty()) {
auto [i, j] = q.front();
q.pop();
for (const auto [di, dj]: directions) {
int ni = i + di, nj = j + dj;
if (ni >= 0 && ni < n && nj >= 0 && nj < n) {
if (visited[ni][nj] == 0 && grid[ni][nj] <= threshold) {
q.push(make_pair(ni, nj));
visited[ni][nj] = 1;
}
}
}
}
return visited[n - 1][n - 1] == 1;
}
int swimInWater2(vector<vector<int>>& grid) {
int n = grid.size();
int left = 0, right = n * n - 1;
while (left < right) {
int mid = (left + right) / 2;
if (check(grid, mid)) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
};