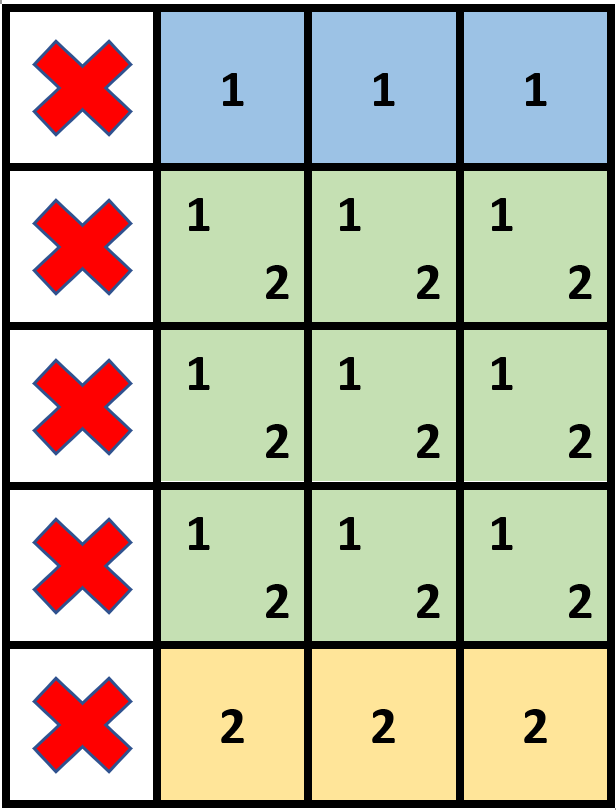
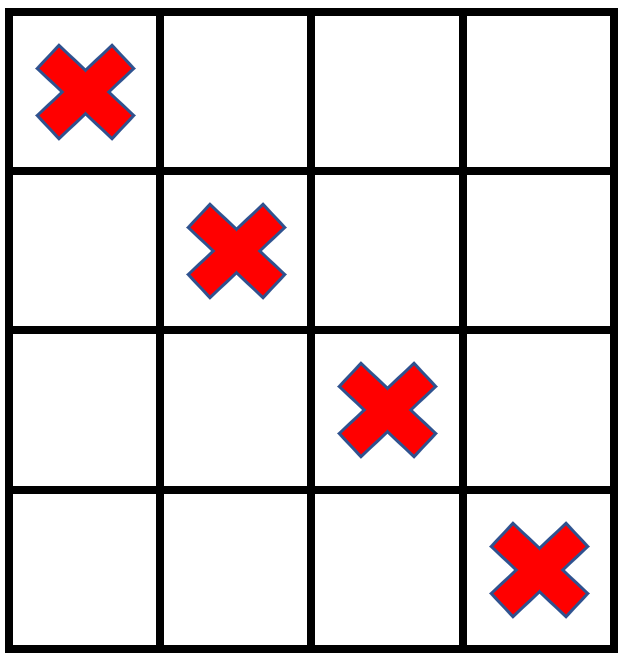
C++
Java
Python
Python3
C
C#
JavaScript
Ruby
Swift
Go
Scala
Kotlin
Rust
PHP
TypeScript
Racket
Erlang
Elixir
Dart
monokai
ambiance
chaos
chrome
cloud9_day
cloud9_night
cloud9_night_low_color
clouds
clouds_midnight
cobalt
crimson_editor
dawn
dracula
dreamweaver
eclipse
github
github_dark
gob
gruvbox
gruvbox_dark_hard
gruvbox_light_hard
idle_fingers
iplastic
katzenmilch
kr_theme
kuroir
merbivore
merbivore_soft
mono_industrial
nord_dark
one_dark
pastel_on_dark
solarized_dark
solarized_light
sqlserver
terminal
textmate
tomorrow
tomorrow_night
tomorrow_night_blue
tomorrow_night_bright
tomorrow_night_eighties
twilight
vibrant_ink
xcode
上次编辑到这里,代码来自缓存 点击恢复默认模板
class Solution {
public:
bool possibleToStamp(vector<vector<int>>& grid, int stampHeight, int stampWidth) {
}
};
运行代码
提交
rust 解法, 执行用时: 60 ms, 内存消耗: 18.7 MB, 提交时间: 2023-12-14 07:45:38
impl Solution {
pub fn possible_to_stamp(grid: Vec<Vec<i32>>, stamp_height: i32, stamp_width: i32) -> bool {
let m = grid.len();
let n = grid[0].len();
// 1. 计算 grid 的二维前缀和
let mut s = vec![vec![0; n + 1]; m + 1];
for (i, row) in grid.iter().enumerate() {
for (j, &v) in row.iter().enumerate() {
s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + v;
}
}
// 2. 计算二维差分
// 为方便第 3 步的计算,在 d 数组的最上面和最左边各加了一行(列),所以下标要 +1
let mut d = vec![vec![0; n + 2]; m + 2];
for i2 in stamp_height as usize..=m {
for j2 in stamp_width as usize..=n {
let i1 = i2 - stamp_height as usize + 1;
let j1 = j2 - stamp_width as usize + 1;
if s[i2][j2] - s[i2][j1 - 1] - s[i1 - 1][j2] + s[i1 - 1][j1 - 1] == 0 {
d[i1][j1] += 1;
d[i1][j2 + 1] -= 1;
d[i2 + 1][j1] -= 1;
d[i2 + 1][j2 + 1] += 1;
}
}
}
// 3. 还原二维差分矩阵对应的计数矩阵(原地计算)
for (i, row) in grid.iter().enumerate() {
for (j, &v) in row.iter().enumerate() {
d[i + 1][j + 1] += d[i + 1][j] + d[i][j + 1] - d[i][j];
if v == 0 && d[i + 1][j + 1] == 0 {
return false;
}
}
}
true
}
}
javascript 解法, 执行用时: 332 ms, 内存消耗: 102.9 MB, 提交时间: 2023-12-14 07:45:25
/**
* @param {number[][]} grid
* @param {number} stampHeight
* @param {number} stampWidth
* @return {boolean}
*/
var possibleToStamp = function (grid, stampHeight, stampWidth) {
const m = grid.length, n = grid[0].length;
// 1. 计算 grid 的二维前缀和
const s = Array(m + 1).fill(null).map(() => Array(n + 1).fill(0));
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + grid[i][j];
}
}
// 2. 计算二维差分
// 为方便第 3 步的计算,在 d 数组的最上面和最左边各加了一行(列),所以下标要 +1
const d = Array(m + 2).fill(null).map(() => Array(n + 2).fill(0));
for (let i2 = stampHeight; i2 <= m; i2++) {
for (let j2 = stampWidth; j2 <= n; j2++) {
const i1 = i2 - stampHeight + 1;
const j1 = j2 - stampWidth + 1;
if (s[i2][j2] - s[i2][j1 - 1] - s[i1 - 1][j2] + s[i1 - 1][j1 - 1] === 0) {
d[i1][j1]++;
d[i1][j2 + 1]--;
d[i2 + 1][j1]--;
d[i2 + 1][j2 + 1]++;
}
}
}
// 3. 还原二维差分矩阵对应的计数矩阵(原地计算)
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
d[i + 1][j + 1] += d[i + 1][j] + d[i][j + 1] - d[i][j];
if (grid[i][j] === 0 && d[i + 1][j + 1] === 0) {
return false;
}
}
}
return true;
};
cpp 解法, 执行用时: 440 ms, 内存消耗: 179.3 MB, 提交时间: 2023-12-14 07:44:52
class Solution {
public:
bool possibleToStamp(vector<vector<int>> &grid, int stampHeight, int stampWidth) {
int m = grid.size(), n = grid[0].size();
// 1. 计算 grid 的二维前缀和
vector<vector<int>> s(m + 1, vector<int>(n + 1));
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + grid[i][j];
}
}
// 2. 计算二维差分
// 为方便第 3 步的计算,在 d 数组的最上面和最左边各加了一行(列),所以下标要 +1
vector<vector<int>> d(m + 2, vector<int>(n + 2));
for (int i2 = stampHeight; i2 <= m; i2++) {
for (int j2 = stampWidth; j2 <= n; j2++) {
int i1 = i2 - stampHeight + 1;
int j1 = j2 - stampWidth + 1;
if (s[i2][j2] - s[i2][j1 - 1] - s[i1 - 1][j2] + s[i1 - 1][j1 - 1] == 0) {
d[i1][j1]++;
d[i1][j2 + 1]--;
d[i2 + 1][j1]--;
d[i2 + 1][j2 + 1]++;
}
}
}
// 3. 还原二维差分矩阵对应的计数矩阵(原地计算)
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
d[i + 1][j + 1] += d[i + 1][j] + d[i][j + 1] - d[i][j];
if (grid[i][j] == 0 && d[i + 1][j + 1] == 0) {
return false;
}
}
}
return true;
}
};
java 解法, 执行用时: 22 ms, 内存消耗: 97.7 MB, 提交时间: 2023-12-14 07:44:37
class Solution {
public boolean possibleToStamp(int[][] grid, int stampHeight, int stampWidth) {
int m = grid.length;
int n = grid[0].length;
// 1. 计算 grid 的二维前缀和
int[][] s = new int[m + 1][n + 1];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + grid[i][j];
}
}
// 2. 计算二维差分
// 为方便第 3 步的计算,在 d 数组的最上面和最左边各加了一行(列),所以下标要 +1
int[][] d = new int[m + 2][n + 2];
for (int i2 = stampHeight; i2 <= m; i2++) {
for (int j2 = stampWidth; j2 <= n; j2++) {
int i1 = i2 - stampHeight + 1;
int j1 = j2 - stampWidth + 1;
if (s[i2][j2] - s[i2][j1 - 1] - s[i1 - 1][j2] + s[i1 - 1][j1 - 1] == 0) {
d[i1][j1]++;
d[i1][j2 + 1]--;
d[i2 + 1][j1]--;
d[i2 + 1][j2 + 1]++;
}
}
}
// 3. 还原二维差分矩阵对应的计数矩阵(原地计算)
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
d[i + 1][j + 1] += d[i + 1][j] + d[i][j + 1] - d[i][j];
if (grid[i][j] == 0 && d[i + 1][j + 1] == 0) {
return false;
}
}
}
return true;
}
}
python3 解法, 执行用时: 988 ms, 内存消耗: 57.1 MB, 提交时间: 2023-12-14 07:44:23
class Solution:
def possibleToStamp(self, grid: List[List[int]], stampHeight: int, stampWidth: int) -> bool:
m, n = len(grid), len(grid[0])
# 1. 计算 grid 的二维前缀和
s = [[0] * (n + 1) for _ in range(m + 1)]
for i, row in enumerate(grid):
for j, v in enumerate(row):
s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + v
# 2. 计算二维差分
# 为方便第 3 步的计算,在 d 数组的最上面和最左边各加了一行(列),所以下标要 +1
d = [[0] * (n + 2) for _ in range(m + 2)]
for i2 in range(stampHeight, m + 1):
for j2 in range(stampWidth, n + 1):
i1 = i2 - stampHeight + 1
j1 = j2 - stampWidth + 1
if s[i2][j2] - s[i2][j1 - 1] - s[i1 - 1][j2] + s[i1 - 1][j1 - 1] == 0:
d[i1][j1] += 1
d[i1][j2 + 1] -= 1
d[i2 + 1][j1] -= 1
d[i2 + 1][j2 + 1] += 1
# 3. 还原二维差分矩阵对应的计数矩阵(原地计算)
for i, row in enumerate(grid):
for j, v in enumerate(row):
d[i + 1][j + 1] += d[i + 1][j] + d[i][j + 1] - d[i][j]
if v == 0 and d[i + 1][j + 1] == 0:
return False
return True
python3 解法, 执行用时: 1664 ms, 内存消耗: 57.9 MB, 提交时间: 2023-08-22 09:58:10
'''
1 在矩阵中标记所有的可放置邮票的区域;
2 对矩阵求二维前缀和;
3 检查矩阵中是否存在值为 000 的点。如果存在,那么该点无法被邮票覆盖。
'''
class Solution:
def possibleToStamp(self, grid: List[List[int]], stampHeight: int, stampWidth: int) -> bool:
m, n = len(grid), len(grid[0])
sums = [[0] * (n + 1) for _ in range(m + 1)]
def build(arr):
for x in range(1, m + 1):
for y in range(1, n + 1):
arr[x][y] = arr[x][y] + arr[x-1][y] + arr[x][y-1] - arr[x-1][y-1]
for x in range(1, m + 1):
for y in range(1, n + 1):
sums[x][y] = grid[x-1][y-1]
build(sums)
diff = [[0] * (n + 2) for _ in range(m + 2)]
for x2 in range(stampHeight, m + 1):
for y2 in range(stampWidth, n + 1):
x1, y1 = x2 - stampHeight, y2 - stampWidth
if sums[x2][y2] - sums[x1][y2] - sums[x2][y1] + sums[x1][y1] == 0:
diff[x1+1][y1+1] += 1
diff[x2+1][y1+1] -= 1
diff[x1+1][y2+1] -= 1
diff[x2+1][y2+1] += 1
build(diff)
for x in range(1, m + 1):
for y in range(1, n + 1):
if grid[x-1][y-1] == 0 and diff[x][y] == 0:
return False
return True
golang 解法, 执行用时: 420 ms, 内存消耗: 21.2 MB, 提交时间: 2023-08-22 09:56:41
/**
* 在矩阵中标记所有的可放置邮票的区域;
* 对矩阵求二维前缀和;
* 检查矩阵中是否存在值为 000 的点。如果存在,那么该点无法被邮票覆盖。
*/
func possibleToStamp(grid [][]int, h int, w int) bool {
m, n := len(grid), len(grid[0])
// 前缀和数组
preSum := make([][]int, m+1)
for i := range preSum {
preSum[i] = make([]int, n+1)
}
// 差分数组
diff := make([][]int, m+2)
for i := range diff {
diff[i] = make([]int, n+2)
}
for i:=1; i<=m; i++ {
for j:=1; j<=n; j++ {
preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] - preSum[i-1][j-1] + grid[i-1][j-1]
}
}
for i:=h; i<=m; i++ {
for j:=w; j<=n; j++ {
cnt := preSum[i][j] - preSum[i-h][j] - preSum[i][j-w] + preSum[i-h][j-w]
if 0 == cnt {
diff[i-h+1][j-w+1]++
diff[i+1][j-w+1]--
diff[i-h+1][j+1]--
diff[i+1][j+1]++
}
}
}
for i:=1; i<=m; i++ {
for j:=1; j<=n; j++ {
diff[i][j] += diff[i][j-1]
}
}
for i:=1; i<=m; i++ {
for j:=1; j<=n; j++ {
diff[i][j] += diff[i-1][j]
if grid[i-1][j-1] == 0 && diff[i][j] == 0 {
return false
}
}
}
return true;
}
golang 解法, 执行用时: 396 ms, 内存消耗: 32.2 MB, 提交时间: 2023-08-22 09:54:32
func possibleToStamp(grid [][]int, stampHeight, stampWidth int) bool {
m, n := len(grid), len(grid[0])
sum := make([][]int, m+1)
sum[0] = make([]int, n+1)
diff := make([][]int, m+1)
diff[0] = make([]int, n+1)
for i, row := range grid {
sum[i+1] = make([]int, n+1)
for j, v := range row { // grid 的二维前缀和
sum[i+1][j+1] = sum[i+1][j] + sum[i][j+1] - sum[i][j] + v
}
diff[i+1] = make([]int, n+1)
}
for i, row := range grid {
for j, v := range row {
if v == 0 {
x, y := i+stampHeight, j+stampWidth // 注意这是矩形右下角横纵坐标都 +1 后的位置
if x <= m && y <= n && sum[x][y]-sum[x][j]-sum[i][y]+sum[i][j] == 0 {
diff[i][j]++
diff[i][y]--
diff[x][j]--
diff[x][y]++ // 更新二维差分
}
}
}
}
// 还原二维差分矩阵对应的计数矩阵,这里用滚动数组实现
cnt := make([]int, n+1)
pre := make([]int, n+1)
for i, row := range grid {
for j, v := range row {
cnt[j+1] = cnt[j] + pre[j+1] - pre[j] + diff[i][j]
if cnt[j+1] == 0 && v == 0 {
return false
}
}
cnt, pre = pre, cnt
}
return true
}
python3 解法, 执行用时: 1320 ms, 内存消耗: 51.1 MB, 提交时间: 2023-08-22 09:54:01
'''
二维前缀和 + 二维差分
'''
class Solution:
def possibleToStamp(self, grid: List[List[int]], stampHeight: int, stampWidth: int) -> bool:
m, n = len(grid), len(grid[0])
sum = [[0] * (n + 1) for _ in range(m + 1)]
diff = [[0] * (n + 1) for _ in range(m + 1)]
for i, row in enumerate(grid):
for j, v in enumerate(row): # grid 的二维前缀和
sum[i + 1][j + 1] = sum[i + 1][j] + sum[i][j + 1] - sum[i][j] + v
for i, row in enumerate(grid):
for j, v in enumerate(row):
if v == 0:
x, y = i + stampHeight, j + stampWidth # 注意这是矩形右下角横纵坐标都 +1 后的位置
if x <= m and y <= n and sum[x][y] - sum[x][j] - sum[i][y] + sum[i][j] == 0:
diff[i][j] += 1
diff[i][y] -= 1
diff[x][j] -= 1
diff[x][y] += 1 # 更新二维差分
# 还原二维差分矩阵对应的计数矩阵,这里用滚动数组实现
cnt, pre = [0] * (n + 1), [0] * (n + 1)
for i, row in enumerate(grid):
for j, v in enumerate(row):
cnt[j + 1] = cnt[j] + pre[j + 1] - pre[j] + diff[i][j]
if cnt[j + 1] == 0 and v == 0:
return False
cnt, pre = pre, cnt
return True