二维网格迁移

1260. 二维网格迁移

给你一个 m 行 n 列的二维网格 grid 和一个整数 k。你需要将 grid 迁移 k 次。

每次「迁移」操作将会引发下述活动：

位于 grid[i][j] 的元素将会移动到 grid[i][j + 1]。
位于 grid[i][n - 1] 的元素将会移动到 grid[i + 1][0]。
位于 grid[m - 1][n - 1] 的元素将会移动到 grid[0][0]。

请你返回 k 次迁移操作后最终得到的 二维网格。

示例 1：

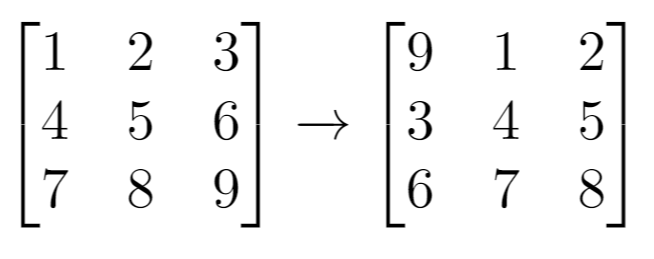
输入：grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1
输出：[[9,1,2],[3,4,5],[6,7,8]]

示例 2：

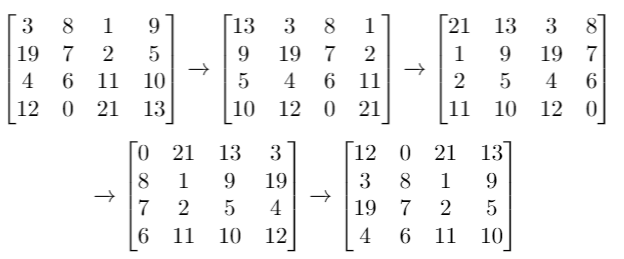
输入：grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4
输出：[[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]

示例 3：

输入：grid = [[1,2,3],[4,5,6],[7,8,9]], k = 9
输出：[[1,2,3],[4,5,6],[7,8,9]]

提示：

m == grid.length
n == grid[i].length
1 <= m <= 50
1 <= n <= 50
-1000 <= grid[i][j] <= 1000
0 <= k <= 100

原站题解

去查看

上次编辑到这里，代码来自缓存点击恢复默认模板

class Solution { public: vector<vector<int>> shiftGrid(vector<vector<int>>& grid, int k) { } };

python3 解法, 执行用时: 48 ms, 内存消耗: 15.4 MB, 提交时间: 2022-08-05 15:02:13

class Solution:
    def shiftGrid(self, grid: List[List[int]], k: int) -> List[List[int]]:
        m, n = len(grid), len(grid[0])
        ans = [[0] * n for _ in range(m)]
        for i, row in enumerate(grid):
            for j, v in enumerate(row):
                index1 = (i * n + j + k) % (m * n)
                ans[index1 // n][index1 % n] = v
        return ans

上一题

下一题

详情